Journal of Mathematical Sciences: Advances and Applications[1] Q. H. Ansari, A. Idzik and J. C. Yao, Coincidence and fixed point
theorems with applications, Topol. Methods Nonlinear Anal. 15 (2000),
191-202.
[2] C. Berge, Topological Spaces, Oliver and Boyd, Edinburgh,
Scotland, 1963.
[3] X. P. Ding, New H-KKM theorems and their applications to geometric
property, coincidence theorems, minimax inequality and maximal
elements, Indian J. Pure Appl. Math. 26 (1995), 1-19.
[4] A. Idzik, Fixed point theorems for families of functions, Bull.
Acad. Polon. Sci. Ser. Sci. Math. Astronom. Phys. 26 (1978),
913-916.
[5] T. Y. Kuo, J. C. Jeng and Y. Y. Huang, Fixed point theorems for
compact multimaps on almost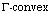 
sets in generalized convex spaces, Nonlinear
Analysis 66 (2007), 415-426.
[6] K. Q. Lan and J. Webb, New fixed point theorems for a family of
mappings and applications to problems on sets with convex sections,
Proc. Amer. Math. Soc. 126 (1998), 1127-1132.
[7] T. W. Ma, On sets with convex sections, J. Math. Anal. Appl. 27
(1969), 413-416.
[8] S. Park, Continuous selection theorems in generalized convex
spaces, Numer. Funct. Anal. Optimi. 20 (1999), 567-583.
[9] S. Park and H. Kim, Coincidence theorems for admissible
multifunctions on generalized convex spaces, J. Math. Anal. Appl. 197
(1996), 173-187.
[10] K. K. Tan and X. L. Zhang, Fixed point theorems on
G-convex spaces and applications, Proceedings of Nonlinear
Functional Analysis and Applications, Vol. 1, Kyungnam University,
Masan, Korea, 1996, pp.1-19.
[11] W. Rudin, Functional Analysis, Second Edition, McGraw-Hill, Inc.,
1991.
