[1] K. Goebel and W. A. Kirk, A fixed point theorem for asymptotically
nonexpansive mappings, Proc. Amer. Math. Soc. 35 (1972), 171-174,
doi:10.1090/S0002-9939-1972-0298500-3.
[2] W. A. Kirk, Fixed point theorems for non-Lipschitzian mappings of
asymptotically nonexpansive type, Israel J. Math. 17(4) (1974),
339-346, doi:10.1007/BF02757136.
[3] R. E. Bruck, Y. Kuczumow and S. Reich, Convergence of iterates of
asymptotically nonexpansive mappings in Banach spaces with the uniform
Opial property, Colloq. Math. 65(2) (1993), 169-179.
[4] U. Kohlenbach, Some logical metatheorems with applications in
functional analysis, Trans. Amer. Math. Soc. 357(1) (2005), 89-128.
[5] K. Goebel and W. A. Kirk, Iteration processes for non-expansive
mappings, In: S. P. Singh, S. Thomeier and B. Watson (Eds.),
Topological methods in nonlinear functional analysis (Toronto, 1982),
Contemporary Mathematics, Vol. 21, pp. 115-123, American Mathematical
Society, Providence, RI, 1983.
[6] S. Reich and I. Shafrir, Nonexpansive iterations in hyperbolic
spaces, Nonlinear Anal.: Theory, Methods Appl. 15 (1990), 537-338.
[7] M. Bridson and A. Haeiger, Metric spaces of non-positive
curvature, Grundlehren der Mathematischen Wissenschaften, Springer,
Berlin, 319 (1999).
[8] T. C. Lim, Remarks on some fixed point theorems, Proc. Amer. Math.
Soc. 60 (1976), 179-182.
[9] W. A. Kirk and B. Panyanak, A concept of convergence in geodesic
spaces, Nonlinear Anal.: Theory, Methods Appl. 68(12) (2008),
3689-3696.
[10] S. Dhompongsa, W. A. Kirk and B. Panyanak, Nonexpansive
set-valued mappings in metric and Banach spaces, J. Nonlinear Convex
Anal. 8(1) (2007), 35-45.
[11] S. Dhompongsa and B. Panyanak, On 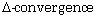 theorems in CAT(0) spaces, Comput. Math.
Appl. 56(10) (2008), 2572-2579.
theorems in CAT(0) spaces, Comput. Math.
Appl. 56(10) (2008), 2572-2579.
[12] W. Laowang and B. Panyanak, Approximating fixed points of
nonexpansive non-self mappings in CAT(0) spaces, Fixed Point Theory
Appl. (2010), Article ID 367274, doi:10.1155/2010/367274.
[13] N. Shahzad, Invariant approximations in CAT(0) spaces, Nonlinear
Anal.: Theory, Methods Appl. 70(12) (2009), 4338-4340.
[14] A. Akbar and M. Eslamian, Fixed point and convergence theorems
for different classes of generalized nonexpansive mappings in CAT(0)
spaces, Comput. Math. Appl. (2012),
doi:10.1016/j.camwa.2011.12.075.
[15] A. R. Khan and M. A. Ahmed, Convergence of a general iterative
scheme for a finite family of asymptotically quasi-nonexpansive
mappings in convex metric spaces and applications, Comput. Math. Appl.
59 (2010), 2990-2995.
[16] K. Goebel and S. Reich, Uniform Convexity, Hyperbolic Geometry,
and Nonexpansive Mappings, Marcel Dekker, New York, 1984.
[17] L. Leustean, A quadratic rate of asymptotic regularity for
CAT(0)-spaces, J. Math. Anal. Appl. 325 (2007), 386-399,
doi:10.1016/j.jmaa.2006.01.081.
[18] L. Leustean, Nonexpansive iterations in uniformly convex
W-hyperbolic spaces, in: A. Leizarowitz, B. S. Mordukhovich, I.
Shafrir and A. Zaslavski (Eds.), Nonlinear Analysis and Optimization
I: Nonlinear Analysis, Contemporary Mathematics (AMS) 513 (2010),
193-209.
[19] S. Dhompongsa, W. A. Kirk and B. Sims, Fixed points of uniformly
Lipschitzian mappings, Nonlinear Anal. 65 (2006), 762-772,
doi:10.1016/j.na.2005.09.044.
[20] A. R. Khan, H. Fukhar-ud-din and M. A. A. Khan, An implicit
algorithm for two finite families of nonexpansive maps in hyperbolic
spaces, Fixed Point Theory Appl. 54 (2012),
doi:10.1186/1687-1812-2012-54.
[21] J. Zhang and Y. Cui, Existence and convergence of fixed points
for mappings of asymptotically nonexpansive type in uniformly convex
W-hyperbolic spaces, Fixed Point Theory Appl. 39 (2011),
doi:10.1186/1687-1812-2011-39.
[22] K. K. Tan and H. K. Xu, Approximating fixed points of
nonexpansive mappings by the Ishikawa iteration process, J. Math.
Anal. Appl. 178 (1993), 301-308.