Journal of Mathematical Sciences: Advances and Applications[1] P. J. Caudrey, R. K. Dodd and J. D. Gibbon, A new heirarchy of
Korteweg-de Vries equation, Proc. Roy. Soc. Lond. A 351 (1976),
407-422.
[2] J. M. Dye and A. Parker, On bidirectional nonlinear fifth-order
nonlinear evolution equations, Lax pairs, and directionally dependent
solitary waves, J. Math. Phys 42 (2001), 2567-2589.
[3] C. A. Gomez, Special forms of the fifth-order KdV equation with
new periodic and soliton solutions, Appl. Math. Comp. 189 (2007),
1066-1077.
[4] A. Karasu Kalcanli, A. Karasu, A. Sakovich, S. Sakovich and R.
Turhan, A new integrable generalization of the Korteweg-de Vries
equation, ar.Xiv:nlin 0708.3247 v1.[nlin.SI] 23 Aug. 2007.
[5] A. Karasu-Kalcanli and S. Sakovich, Bäcklund transformation and
special solutions for the Drinfeld-Sokolev-Satsuma-Hirota system of
coupled equations, J. Phys. A Math. Gen. 34 (2001), 7355-7358.
[6] D. J. Kaup, On the inverse scattering problem for cubic eingevalue
problems of the class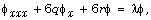 
Stud. Appl. Math. 62 (1980), 189-216.
[7] B. A. Kupershmidt, KdV6: An Integrable System, arXiv: nlin
0709.3848v1.[nlin.SI] 24 Sep. 2007.
[8] K. Sawada and T. Kotera, A method for finding N-soliton solutions
for the KdV equation and Kdv-like equation, Prog. Theory, Phys. 51
(1974), 1355-1367.
[9] C. Verhoeven and M. Musette, Soliton solutions of two
bidirectional sixth order partial differential equations belonging to
the KP hierarchy, J. Phys. A Math. Gen. 36 (2003), L133-L143.
[10] A. M. Wazwaz, The extended tanh method for new solitons solutions
for many forms of the fifth-order KdV equations, Appl. Math. Comput.
84(2) (2007), 1002-1014.
