Journal of Mathematical Sciences: Advances and Applications[1] M. Brešar, Jordan derivations on semiprime rings, Proc. Amer.
Math. Soc. 104 (1988), 1003-1006.
[2] M. Brešar, Characterizing homomorphisms, derivations and
multipliers in rings with idempotents, Proc. R. Soc. Edinb., Sect. A
137 (2007), 9-21.
[3] J. A. Brooke, P. Busch and B. Pearson, Commutativity up to a
factor of bounded operators in complex Hilbert spaces, R. Soc. Lond.
Proc. Ser. A Math Phys. Eng. Sci. A 458 (2002), 109-118.
[4] I. N. Herstein, Jordan derivations of prime rings, Proc. Amer.
Math. Soc. 8 (1957), 1104-1110.
[5] J. C. Hou and X. F. Qi, Additive maps derivable at some points on
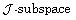lattice algebras, Lin. Alg. Appl. 429
(2008), 1851-1863.
[6] B. E. Johnson, Symmetric amenability and the non-existence of Lie
and Jordan derivations, Math. Proc. Cambridge Philos. Soc. 120 (1996),
455-473.
[7] P. S. Ji and W. Q. Qi, Characterizations of Lie derivations of
triangular algebras, Linear Algebra and its Applications 435(5)
(2011), 1137-1146.
[8] C. Kassel, Quantum Groups, Springer-Verlag, New York, 1995.
[9] L. Liu and G. X. Ji,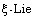 
derivable maps and generalized 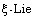derivable maps on standard operator
algebras, Preprint.
[10] F. Lu and W. Ji, Characterizations of Lie derivations of
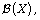Lin. Alg. Appl. 432 (2009), 89-99.
[11] M. Mathieu and A. R. Villena, The structure of Lie derivations on
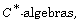J. Funct. Anal. 202 (2003), 504-525.
[12] C. R. Miers, Lie isomorphisms of operator algebras, Pacific J.
Math. 38 (1971), 717-735.
[13] X. F. Qi and J. C. Hou, Additive Lie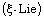 
derivations and generalized Lie 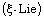derivations on Nest algebras, Lin. Alg.
Appl. 431 (2009), 843-854.
[14] X. F. Qi and J. C. Hou, Linear maps Lie derivable at zero on
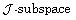lattice algebras, Studia Math. 197 (2010),
157-169.
[15] X. F. Qi and J. C. Hou, Characterization of Lie derivations on
prime rings, Communication in Algebras 39(10) (2011), 3824-3835.
[16] X. F. Qi, J. Cui and J. C. Hou, Characterizing additive
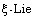derivations of prime algebras by 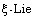zero products, Lin. Alg. Appl. 434 (2011),
669-682.
[17] X. F. Qi and J. C. Hou, Additive Lie 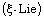derivations and generalized Lie 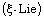derivations on prime algebras, Acta Math.
Sin., English Series 29(2) (2013), 383-392.
[18] W. L. Yang and J. Zhu, Characterizations of additive
(generalized)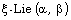 
derivations on triangular algebras, Linear
and Multilinear Algebras 61(6) (2013), 811-830.
