Journal of Mathematical Sciences: Advances and Applications[1] E. Al-Shemas and S. Billups, An iterative method for generalized
set-valued nonlinear mixed quasi-variational inequalities, J. Comp.
Appl. Math. 170 (2004), 423-432.
[2] E. Al-Shemas, Wiener-Hopf equations technique for multivalued
general variational inequalities, J. Adv. Math. Stud. 2(2) (2009),
01-08.
[3] E. Al-Shemas, Projection iterative methods for multivalued general
variational inequalities, Appl. Math. & Inform. Sci. 3(2) (2009),
177-184.
[4] M. Bounkhel, L. Tadj and A. Hamdi, Iterative schemes to solve
nonconvex variational problems, J. Inequal. Pure Appl. Math. 4 (2003),
1-14.
[5] F. H. Clarke, R. J. Stern and P. R. Wolenski, Proximal smoothness
and the lower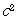 
property, J. Convex Anal. 2(1/2) (1995),
117-144.
[6] F. H. Clarke, Y. S. Ledyaev and P. R. Wolenski, Nonsmooth Analysis
and Control Theory, Springer-Verlag, Berlin, 1998.
[7] D. Kinderlehrer and G. Stampacchia, An Introduction to Variational
Inequalities and their Applications, SIAM, Philadelphia, 2000.
[8] J. L. Lions and G. Stampacchia, Variational inequalities, Comm.
Pure Appl. Math. 20 (1967), 493-512.
[9] A. Moudafi, An algorithmic approach to prox-regular variational
inequalities, Appl. Math. Comput. 155(3) (2004), 845-852.
[10] M. Aslam Noor, Iterative schemes for nonconvex variational
inequalities, J. Optim. Theory Appl. 121 (2004), 385-395.
[11] M. Aslam Noor, Strongly nonlinear nonconvex variational
inequalities, J. Adv. Math. Stud. 4(1) (2011), 77-84.
[12] M. Aslam Noor, Nonconvex Wiener-Hopf equations and variational
inequalities, to appear.
[13] L. P. Pang, J. Shen and H. S. Song, A modified
predictor-corrector algorithm for solving nonconvex generalized
variational inequalities, Computers Math. Appl. 54 (2007), 319-325.
[14] R. A. Poliquin, R. T. Rockafellar and L. Thibault, Local
differentiability of distance functions, Trans. Amer. Math. Soc. 352
(2000), 5231-5249.
[15] S. Shi, Equivalence of variational inequalities with Wiener-Hopf
equations, Proc. Amer. Math. Soc. 111 (1991), 439-446.
[16] G. Stampacchia, Formes bilineaires coercitives sur les ensembles
convexes, C. R. Acad. Sci., Paris, 258 (1964), 4413-4416.
