Journal of Mathematical Sciences: Advances and Applications[1] C. Carathéodory, Vorlesungen Iuber Reellen Funktionen, Leipzig
and Berlin, 1918.
[2] J. R. Christensen, Measure theoretic zero sets in infinite
dimensional spaces and applications to differentiability of Lipschitz
mappings, Actes du Deuxieme Colloque d’Analyse Fonctionnelle de
Bordeaux (Univ. Bordeaux, 1973), I, pp. 29-39, Publ. Dep. Math. (Lyon)
10(2) (1973), 29-39.
[3] M. Csörnyei, Aronszajn null and Gaussian null sets coincide,
Israel J. Math. 111 (1999), 191-201.
[4] R. Dougherty, Examples of non-shy sets, Fund. Math. 144 (1994),
73-88.
[5] F. Hausdorff, Mengenlehre, 3rd Edition, Berlin, 1935.
[6] B. R. Hunt, T. Sauer and J. A. Yorke, Prevalence: A
Translation-Invariant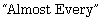 
on Infinite-Dimensional Spaces, Bulletin
(New Series) of the American Mathematical Society 27(2) (1992),
217-238.
[7] S. Kakutani, Ober die metrisation der topologischen gruppen, Proc.
Imp. Acad. Tokyo 12 (1936), 82-84.
[8] P. Mankiewicz, On the differentiability of Lipschitz mappings in
Fréchet spaces, Studia Math. 45 (1973), 15-29.
[9] J. Mycielski, Some unsolved problems on the prevalence of
ergodicity, instability, and algebraic independence, Ulam Quart. 1(3)
(1992), 30 ff, approx. 8 pp.
[10] J. C. Oxtoby and S. M. Ulam, On the existence of a measure
invariant under a transformation, Ann. of Math. 40(2) (1939),
560-566.
[11] J. C. Oxtoby, Invariant measures in groups which are not locally
compact, Trans. Amer. Math. Soc. 60 (1946), 215-237.
[12] G. R. Pantsulaia, Invariant and Quasi-Invariant Measures in
Infinite-Dimensional Topological Vector Spaces, Nova Science
Publishers, Inc., New York, 2007.
[13] G. R. Pantsulaia and G. P. Giorgadze, On analogy of Liouville
theorem in infinite-dimensional separable Hilbert space, Georgian Int.
J. Sci. Technol. 1(2) (2008), 167-180.
[14] G. R. Pantsulaia, On a generalized Fourier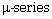 
in some infinite-dimensional Polish
topological vector spaces, Georgian Int. J. Sci. Technol. 1(4) (2008),
313-326.
[15] G. R. Pantsulaia, On generators of shy sets on Polish topological
vector spaces, New York J. Math. 14 (2008), 235-261.
[16] G. R. Pantsulaia and G. P. Giorgadze, On Liouville type theorems
for Mankiewicz and Preiss-Tišer generators in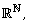 
Georgian Int. J. Sci. Technol. 1(2)
(2009).
[17] G. R. Pantsulaia, On a certain criterion of shyness in the
product of unimodular Polish groups that are not compact, J. Math.
Sci. Adv. Appl. 3(2) (2009), 287-302.
[18] G. R. Pantsulaia, On T-shy sets in Radon metric groups, J. Math.
Sci. Adv. Appl. 5(1) (2010), 149-186.
[19] G. R. Pantsulaia and G. P. Giorgadze, Lebesgue -null sets in
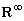are not preserved under Lipschitz
isomorphisms, Georg. Inter. J. Sci. Technol. 3(1) (2011), 39-49.
[20] R. R. Phelps, Gaussian null sets and differentiability of
Lipschitz maps on Banach spaces, Pac. J. Math. 77 (1978), 523-531.
[21] L. Pontrjagin, Topological Groups, Princeton, 1939.
[22] D. Preiss and J. Tišer, Two unexpected examples concerning
differentiability of Lipschitz functions on Banach spaces, Geometric
aspects of functional analysis, (Israel, 1992-1994), 219-238, Oper.
Theory Adv. Appl., Birkhäuser, Basel, 77 (1995).
[23] H. Shi, Measure-Theoretic Notions of Prevalence, Ph.D.
Dissertation (under Brian S. Thomson), Simon Fraser University,
1997.
[24] N. N. Vakhanya, V. I. Tarieladze and S. A. Chobanyan, Probability
Distributions in Banach Spaces, Nauka, Moscow, 1985 (in Russian).
