References

Journal of Mathematical Sciences: Advances and Applications

STRONG CONVERGENCE THEOREMS OF TOTAL NONEXPANSIVE SEMI-GROUPS IN BANACH SPACES

[1] Y. I. Alber, Metric and generalized projection operators in Banach spaces: Properties and applications, A. G. Kartosator (Editor), Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Marcel Dekker, New York, (1996), 15-50.

[2] N. Buong, Hybrid Ishikawa iterative methods for a nonexpansive semigroup in Hilbert space, Comput. Math. Appl. 61 (2011), 2546-2554.

[3] C. Byrne, A unified treatment of some iterative algorithms in signal processing and image construction, Inverse Probl. 20 (2004), 103-120.

[4] S. S. Chang, L. Yang and J. A. Liu, Strong convergence theorem for nonexpansive semi-groups in Banach spaces, Appl. Math. Mech. 28 (2007), 1287-1297.

[5] S. S. Chang, H. W. Joseph Lee and C. K. Chan, Convergence theorem of common fixed point for aysmptotically nonexpansive semi-groups in Banach spaces, Appl. Math. Comput. 212 (2009), 60-65.

[6] S. S. Chang, H. W. Joseph Lee and C. K. Chan, A new hybrid method for solving a generalized equilibrium problem solving a variational inequality problem and obtaining common fixed points in Banach spaces with applications, Nonlinear Anal. TMA 73 (2010), 2260-2270.

[7] S. S. Chang, C. K. Chan and H. W. Joseph Lee, Modified block iterative algorithm for 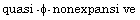mappings and equilibrium problem in Banach spaces, Appl. Math. Comput. 217 (2011), 7520-7530.

[8] S. S. Chang, H. W. Joseph Lee, C. K. Chan and L. Yang, Approximation theorems for total 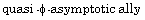nonexpansive mappings with applications, Appl. Math. Comput. 218 (2011), 2921-2931.

[9] Y. J. Cho, L. Ciric and S. H. Wang, Convergence theorems for nonexpansive semi-groups in CAT(0) spaces, Nonlinear Anal. doi: 10.1016/j.na.2011.05.082, (2011).

[10] I. Cioranescu, Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Kluwer Academic, Dordrecht, 1990.

[11] P. L. Combettes, The convex feasibility problem in image recovery, P. Hawkes (Editor), Advances in Imaging and Electron Physics, Academic Press, New York, 95 (1996), 155-270.

[12] B. Halpern, Fixed points of nonexpanding maps, Bull. Amer. Math. Soc. 73 (1967), 957-961.

[13] S. Kitahara and W. Takahashi, Image recovery by convex combinations of sunny nonexpansive retractions, Topol. Methods Nonlinear Anal. 2 (1993), 333-342.

[14] W. R. Mann, Mean value methods in iteration, Proc. Amer. Math. Soc. 4 (1953), 506-510.

[15] K. Nakajo and W. Takahashi, Strong convergence theorems for nonexpansive mappings and nonexpansive semi-groups, J. Math. Anal. Appl. 279 (2003), 372-379.

[16] S. Plubtieng and K. Ungchittrakool, Hybrid iterative methods for convex feasibility problems and fixed point problems of relatively nonexpansive mappings in Banach spaces, Fixed Point Theory Appl., Vol. 2008, Article ID 583082, 19 pages, doi: 10.1155/2008/583082, (2008).

[17] X. L. Qin, Y. J. Cho, S. M. Kang and H. Y. Zhou, Convergence of a modified Halpern-type iterative algorithm for 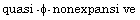mappings, Appl. Math. Lett. 22 (2009), 1051-1055.

[18] T. Suzuki, On strong convergence to common fixed points of nonexpansive semi-groups in Hilbert spaces, Proc. Amer. Math. Soc. 131 (2003), 2133-2136.

[19] D. V. Thong, An implicit iteration process for nonexpansive semigroups, Nonlinear Anal. doi: 10.1016/j.na.2011.05.090, (2011).

[20] H. K. Xu, A strong convergence theorem for contraction semi-groups in Banach spaces, Bull. Austral. Math. Soc. 72 (2005), 371-379.

[21] L. Yang, F. H. Zhao and J. K. Kim, Hybrid projection method for generalized mixed equilibrium problem and fixed point problem of infinite family of asymptotically 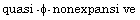mappings in Banach spaces, Appl. Math. Comput. 218 (2012), 6072-6082.

[22] S. S. Zhang, Convergence theorem of common fixed points for Lipschitzian pseudo-contraction semi-groups in Banach spaces, Appl. Math. Mech. 30(2) (2009), 145-152, (English Edition).

[23] H. Y. Zhou, G. Gao and B. Tan, Convergence theorems of a modified hybrid algorithm for a family of 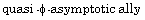nonexpansive mappings, J. Appl. Math. Comput. (2009), doi:10.1007/s12190-009-0263-4.

[24] H. Zhou, G. Gao and B. Tan, Convergence theorems of a modified hybrid algorithm for a family of 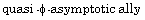nonexpansive mappings, Appl. Math. Comput. 32(2) (2010), 453-464.

[25] J. H. Zhu, S. S. Chang and M. Liu, Generalized mixed equilibrium problems and fixed point problem for a countable family of total 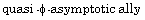nonexpansive mappings in Banach spaces, J. Appl. Math. Vol. 2012, Article ID 961560, 22 pages, doi: 10.1155/2012/9 61560, (2012).