Journal of Pure and Applied Mathematics: Advances and ApplicationsAuthor's: G. I. MIRUMBE, V. A. SSEMBATYA, RIKARD BØGVAD and JAN ERIK BJÖRK
Pages: [135] - [155]
Received Date: November 30, 2011
Submitted by:
Given the following ordinary differential equation:
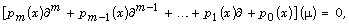(0.1)
where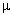 
is a distribution, 
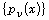are polynomials, which in general may have
complex coefficients, and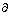 
is the first order derivation operator with
respect to the variable x.
We prove using analytic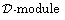 
theory tools that the dimension of the
solution space in the space of distributions is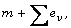 
where the 
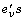are the multiplicities of the real roots
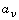of the leading polynomial coefficient
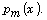This result is an extension of a similar
result highlighted by Mandai [6].
boundary values, distribution solution, characteristic exponents, locally Fuchsian, exact sequences.
