Author's: Shahana Parvin, M. Shamsul Alam Sarker and Shamima Sultana
Pages: [63] - [93]
Received Date: December 3, 2013; Revised January 5, 2014
Submitted by:
Equations of motion in 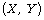 frame moving with the waves are considered
for steady, incompressible flow. The boundary conditions at the bottom
frame moving with the waves are considered
for steady, incompressible flow. The boundary conditions at the bottom
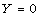 and at the free surface
and at the free surface 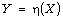 are used for solving shallow water wave
problems. The remaining boundary conditions are also taken from
Navier-Stokes equation of motion. Using these boundary conditions,
three nonlinear ordinary differential equations are formulated, which
can be solved by using series expansion method. We consider that all
variations in X is relatively slow and can be expressed in
terms of dimensionless variable
are used for solving shallow water wave
problems. The remaining boundary conditions are also taken from
Navier-Stokes equation of motion. Using these boundary conditions,
three nonlinear ordinary differential equations are formulated, which
can be solved by using series expansion method. We consider that all
variations in X is relatively slow and can be expressed in
terms of dimensionless variable 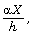 where
where 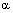 is a small quantity and h is the
trough depth of fluid. Then approaching on series expansion method,
two types of nonlinear ordinary differential equations are formulated.
Using Jacobi elliptic function, first and second order cnoidal wave
solutions have been derived. Then mean value of Jacobi elliptic
function and the solitary wave limit of cnoidal wave solutions are
also formulated.
is a small quantity and h is the
trough depth of fluid. Then approaching on series expansion method,
two types of nonlinear ordinary differential equations are formulated.
Using Jacobi elliptic function, first and second order cnoidal wave
solutions have been derived. Then mean value of Jacobi elliptic
function and the solitary wave limit of cnoidal wave solutions are
also formulated.
Navier-Stokes equation, Jacobi elliptic function, cnoidal wave, solitary wave limit.