Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: HAYKEL GAAYA
Pages: [1] - [19]
Received Date: Received April 19, 2011
Submitted by: Mubariz T. Karaev.
For any n-by-n complex matrix T and any
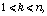let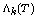 
be the set of all 
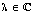such that 
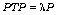for some rank-k orthogonal
projection P be its higher rank-k numerical range. It is
shown that if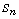 
is the n-dimensional shift on
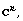then its rank-k numerical range is
the circular disc centered in zero and with radius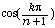 
if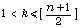 
and the empty set if 
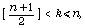where [x] denote the integer part of
x. This extends and refines previous results of Haagerup and de
la Harpe [11] on the classical numerical range of the
n-dimensional shift on 
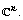An interesting result for higher
rank-k numerical range of nilpotent operator is also
established.
operator theory, numerical radius, numerical range, higher rank numerical range, eigenvalues.
