Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: BANYAT SROYSANG
Pages: [91] - [95]
Received Date: October 15, 2011
Submitted by:
An interior point of a finite planar point set is a point of the set
that is not on the boundary of the convex hull of the set. For any
integer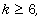 
let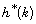 
be the smallest positive integer such that
every planar point set P with no three collinear points and
with at least 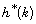interior points has a subset 
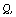whose the interior of the convex hull of
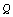contains exactly 4 or 5 or k points
of P. In this paper, we prove that 
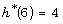and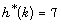 
for all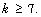 
finite planar point set, interior point, convex hull, deficient point set.
