Author's: Athanasios G. Georgiadis
Pages: [115] - [132]
Received Date: February 28, 2011
Submitted by:
Let M be a Riemannian manifold, which satisfies the doubling
volume property. Let L be a 2m-order differential
operator on M and 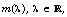 a multiplier satisfying the
Mikhlin-Hörmander condition. We also assume that the associated
heat kernel satisfies a certain upper Gaussian estimate, and we prove
that the spectral multiplier
a multiplier satisfying the
Mikhlin-Hörmander condition. We also assume that the associated
heat kernel satisfies a certain upper Gaussian estimate, and we prove
that the spectral multiplier 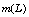 is bounded on
is bounded on 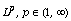 and from
and from 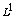 to
to 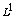 week.
week.
spectral multipliers, higher order differential operators, heat kernels, Riemannian manifolds, Calderon Zygmund decomposition, Hardy-Littlewood maximal function.