Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Abdourahman Haman Adji and Shankishvili Lamara Dmitrievna
Pages: [31] - [52]
Received Date: September 1, 2024
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122310
The main objective set in this research is the construction of
noetherian theory for a singular linear integro-differential operator
L defined by a linear singular differential equation of higher
order in a specific functional space well chosen to achieve the goal.
It should be emphasized that the case where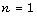 
has been completely studied in the two
situations separately when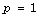 
and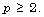 
Our previous various published research was
related to this topic. The methodology adopted on a case-by-case
basis, and depending on the values and sign of the parameter
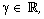leads us to solve the linear differential
equation studied with a well-known second specific right-hand side
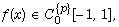systematically identifying the conditions
solvency. This takes us straight to the investigation and construction
of the noetherity (neotherian theory) of the operator L.
Finally, depending on each case, we evaluate and calculate the
deficient numbers and the index of the operator considered in various
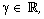situations, relative to the parameter thus, parallel to the construction of the
noetherian theory of the differential operator L, we bring out
the solvability conditions of the equation studied in space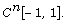 
noetherian theory, third kind integral equation, singular linear integro-differential operator, deficient numbers, index of the operator, associated operator and associated space.
