Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Abdourahman Haman Adji
Pages: [13] - [37]
Received Date: July 28, 2024
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122305
The main purpose of this work is to realize the noetherization
construction theory for an integro-differential operator defined by a
third-kind integral equation in a specific well-chosen functional
space. Several works carried out by our predecessors in connection
with the construction of noetherian theory for integro-differential
operators defined by integral equations of the third kind when the
main part of the operator is defined in the form of the product of a
function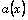 
by the unknown function have been published.
The particularity of our research focuses on the case, where the main
part of the operator A this time contains the product of a
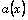function by the derivative of the unknown function
itself. To achieve the noetherization of the operator A, it was
necessary to use a rather special approach involving the notion of
derivative in the Taylor sense of the unknown function. The
noetherization of operator A is constructed and the solvability
conditions of the integral equation have been released. An
illustrative example has been realized at the end of the paper.
noetherian theory, third kind integral equation, singular linear integro-differential operator, characteristic numbers, index of the operator.
