Author's: Fredy Maglorio Sobrado Suárez and Lesly Daiana Barbosa Sobrado
Pages: [17] - [64]
Received Date: April 16, 2023
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122278
In this work, we present the study of the regularity of the solutions
of the abstract system (1) that includes the Euler-Bernoulli
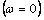 and Kirchhoff-Love
and Kirchhoff-Love 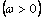 thermoelastic plates, we consider for both
fractional couplings given by
thermoelastic plates, we consider for both
fractional couplings given by 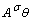 and
and 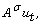 where
where 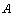 is a strictly positive and self-adjoint linear
operator and the parameter
is a strictly positive and self-adjoint linear
operator and the parameter 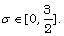 Our research stems from the work of [1], [4],
and [8]. Our contribution was to directly determine the Gevrey sharp
classes: for
Our research stems from the work of [1], [4],
and [8]. Our contribution was to directly determine the Gevrey sharp
classes: for 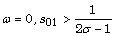 and
and 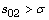 when
when 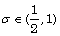 and
and 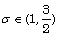 respectively. And
respectively. And 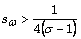 for case
for case 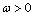 when
when 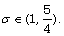 This work also contains direct proofs of the
analyticity of the corresponding semigroups
This work also contains direct proofs of the
analyticity of the corresponding semigroups 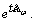 In the case
In the case 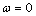 the analyticity of the semigroup
the analyticity of the semigroup 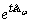 occurs when
occurs when 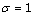 and for the case
and for the case 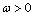 the semigroup
the semigroup 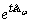 is analytic for the parameter
is analytic for the parameter 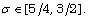 The abstract system is given by:
The abstract system is given by:
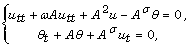 (1)
(1)
where 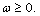
asymptotic behaviour, stability, regularity, Gevrey sharp classes, analyticity, Euler-Bernoulli and Kirchhoff-Love plates.