Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Alexis Nangue, Abdou Ousman and Idrissou Mohamadou
Pages: [1] - [36]
Received Date: September 18, 2021; Revised December 24, 2021
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122228
This work proposes and investigates a delayed cell population model of
hepatitis B virus (HBV) infection. We use the Hattaf-Yousfi incidence
function to describe viral infection. The model takes into account a
specific functional response and the usually neglected absorption
effect. Moreover, we introduce a time delay to account for the
transformation processes necessary for actual HBV production. We
naturally find a threshold parameter, namely, the basic reproduction
number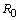 
which ultimately determines the stability of
the equilibria of the model obtained under other conditions. We
determine the equilibria of our model known as uninfected equilibrium
and infected equilibrium, and show that the model is well-posed,
mathematically and biologically. By constructing appropriate Lyapunov
functionals and using LaSalle’s invariance principle, we show
that, if 
the uninfected equilibrium is globally
asymptotically stable. Furthermore, we prove that the uninfected
equilibrium is locally asymptotically stable if 
Hattaf-Yousfi functional response, hepatitis B virus, absorption effect, Lyapunov functional, stability.
