Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Yolanda Silvia Santiago Ayala and Santiago Cesar Rojas Romero
Pages: [1] - [19]
Received Date: November 25, 2020
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122161
In this article, we prove that initial value problem associated to the
non-homogeneous KdV-Kuramoto-Sivashinsky (KdV-K-S) equation in
periodic Sobolev spaces has a local solution in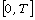 
with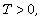 
and the solution has continuous dependence with
respect to the initial data and the non-homogeneous part of the
problem. We do this in an intuitive way using Fourier theory and
introducing a 
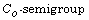inspired by the work of Iorio [2] and Ayala and
Romero [8].
Also, we prove the uniqueness solution of the homogeneous and
non-homogeneous KdV-K-S equation, using its dissipative property,
inspired by the work of Iorio [2] and Ayala and Romero [9].
uniqueness solution, KdV-Kuramoto-Sivashinsky equation, non-homogeneous equation, periodic Sobolev spaces, Fourier theory, calculus in Banach spaces.
