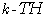 POWER OF STOKES OPERATOR
POWER OF STOKES OPERATORAuthor's: Eleftherios Protopapas
Pages: [1] - [10]
Received Date: June 26, 2020; Revised July 2, 2020
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122139
Stokes operators, 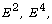 are well known partial differential operators
of elliptic type, which are often used in Applied Mathematics. Stokes
equation
are well known partial differential operators
of elliptic type, which are often used in Applied Mathematics. Stokes
equation 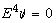 describes the irrotational, axisymmetric
creeping flow and Stokes bi-stream equation
describes the irrotational, axisymmetric
creeping flow and Stokes bi-stream equation 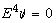 denotes the rotational one, where
denotes the rotational one, where 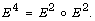 Necessary and sufficient conditions for the
separability and the R-separability of the equation
Necessary and sufficient conditions for the
separability and the R-separability of the equation 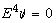 have been proved recently. Moreover, the
0-eigenspace and the generalized 0-eigenspace of the operator
have been proved recently. Moreover, the
0-eigenspace and the generalized 0-eigenspace of the operator
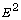 have been derived in several coordinate
systems. Specifically, the spherical coordinate system is employed in
many problems taking into account that in many engineering
applications, the solutions in spherical geometry seem to be adequate
for solving a problem. In the present manuscript, it is shown that
equation
have been derived in several coordinate
systems. Specifically, the spherical coordinate system is employed in
many problems taking into account that in many engineering
applications, the solutions in spherical geometry seem to be adequate
for solving a problem. In the present manuscript, it is shown that
equation 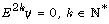 admits a solution of the form
admits a solution of the form 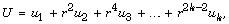 where
where 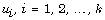 are solutions of Stokes equation and r
is the radial spherical variable. Additionally, we obtain the kernel
of the
are solutions of Stokes equation and r
is the radial spherical variable. Additionally, we obtain the kernel
of the 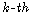 power of the Stokes operator,
power of the Stokes operator, 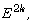 in the spherical geometry for every
in the spherical geometry for every 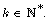
Stokes operator, eigenfunctions, spherical system of coordinates, Gegenbauer functions.