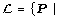Journal of Mathematical Sciences: Advances and Applications
PERFECTLY NORMAL IS STRONGER THAN OR EQUAL TO
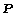AND 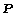IS STRONGER THAN OR EQUAL TO 
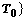WITH THE PARTIAL ORDER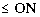 
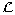DEFINED BY 
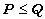IFF 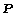IS WEAKER THAN OR EQUAL TO 
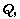AND OTHERSAuthor's: Charles Dorsett
Pages: [39] - [50]
Received Date: December 29, 2019
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122111
In classical topology the separation axioms 
completely Hausdorff, 
were introduced and investigated. Later the
perfectly normal and perfectly Hausdorff separation axioms were added.
In this paper, the mathematical structure of 
perfectly normal is stronger than or equal to
and is stronger than or equal to 
with the partial order 
on 
defined by 
iff is weaker than or equal to 
and others are investigated and shown to be
complete lattices.
no between topological properties, lattice structures in topology.
