Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Halima Nachid, Firmin K. N’gohisse and Yoro Gozo
Pages: [1] - [37]
Received Date: October 10, 2019; Revised November 20, 2019
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122103
In this paper, we study a localized nonlinear reaction diffusion
equation. We investigate interactions among the localized and local
sources, nonlinear diffusion with the zero boundary value condition to
establish the blow-up solution and estimate the numerical
approximation for the following initial-boundary value problem:
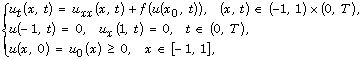
where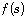 
is a positive, increasing, convex function for
the nonnegative values of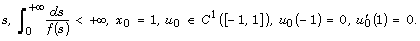 
We find some conditions under which the solution of a discrete form of
the above problem blows up in a finite time and a numerical method is
proposed for estimating its numerical blow-up time. We also prove the
convergence of the numerical blow-up time to the theoretical one.
Finally, we give some numerical results to illustrate our analysis.
discretization, numerical blow-up time, blow-up, Dirichlet, Neumann boundary conditions, convergence, localized nonlinear source term.
