Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Juhani Riihentaus
Pages: [17] - [40]
Received Date: July 31, 2010
Submitted by:
We begin by recalling the definition of nonnegative quasinearly
subharmonic functions on locally uniformly homogeneous spaces. Recall
that these spaces and this function class are rather general: Among
others subharmonic, quasisubharmonic, and nearly subharmonic functions
on domains of Euclidean spaces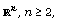 
are included. The following result of
Gehring and Hallenbeck is classical: Every subharmonic function,
defined and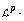 
integrable for some 
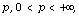on the unit disk 
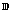of the complex plane 
is for almost all 
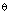of the form 
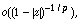uniformly as 
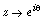in any Stolz domain. Recently, both
Pavlović and Riihentaus have given related and partly more general
results on domains of 
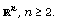Now, we extend one of these results to
quasinearly subharmonic functions on locally uniformly homogeneous
spaces.
locally uniformly homogeneous spaces, subharmonic function, quasinearly subharmonic functions, domain with Ahlfors-regular boundary, generalized mean value inequality, weighted boundary behavior.
