Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Mactar Ndaw, Macoumba Ndour and Papa Ngom
Pages: [75] - [100]
Received Date: September 16, 2018; Revised October 10, 2018
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100122000
In the field of statistical modelling, the distance or divergence
measure is a criterion widely known and widely used tool for
theoretical and applied statistical inference and data processing
problems. In this paper, we deal with the well-known
Alpha-Beta-divergences (which we shall refer to as the
AB-divergences), which are a family of cost functions parametrized by
two hyperparameters and their tight connections with the notions of
Hilbertian metrics and positive definite (pd) kernels on probability
measures. An attempt is made to describe this dissimilarity measure,
which can be symmetrized using its two tuning parameters, alpha and
beta. We compute the degree of symmetry of the AB-divergence on the
basis of Hilbertian metrics. We investigate the desirable properties
that the proposed approach needs to build a positive definite kernel
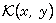corresponding to this symmetric
AB-divergence.
We establish the effectiveness of our approach with experiments
conducted on Support Vector Machine (SVM) and the applicability of
this method is described in an algorithm from this symmetric
divergence in image classification.
We perform experiments using the conditionally defined positive
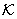and the kernel transformed 
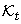and show that these kernels have the same
proportion of errors for the Euclidian divergence and the Hellinger
divergence. We also observe large reductions in error for the
Itakura-Saito divergence with the kernel in classifications than
classical kernel methods.
Hilbertian metrics, positive definite (pd) kernels, divergence, support vector machine (SVM).
