Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Cheikh Seck
Pages: [71] - [101]
Received Date: March 14, 2018; Revised April 3, 2018
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100121939
This work consists on the computation of singularities coefficients in
a non convex plane domain. We use a mixed finite element method of
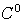class based on a technical characterisation of
dual singular functions. Indeed, these coefficients are obtained
directly from dual singular functions. The operator which used here is
the bilaplacian involved in the problem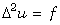 
decomposed in two laplacians 
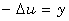and 
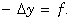Throughout the discretization, the singular
functions are no longer set up on u but on y. In some
regularity conditions, the error estimations for the singular
coefficients with these hypotheses, give us an error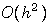 
when we use dual singular functions.
Numerical tests with Free-fem++ allowed us to calculate and plot the
curves of the coefficients of singularities by direct calculations and
approximations using finite elements mixed in the same benchmark.
Thus, it follows asymptotically that the gap between the two curves is
very small narrows and stabilizes when the mesh becomes more refined.
bilaplacian, mixed finite element, singular functions, dual singular functions, error estimations, cracks, simulations, Free-fem++ and Scilab.
