Journal of Mathematical Sciences: Advances and Applications
SHY SETS IN RADON METRIC GROUPSAuthor's: Gogi R. Pantsulaia
Pages: [149] - [185]
Received Date: February 11, 2010
Submitted by:
Let G be a complete metric group and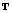 
be such a subgroup of its Borel
automorphisms group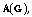 
which contains all left and right shifts of
the G. We introduce notions of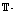 
cm and 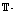shy sets and demonstrate that they constitute
a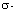 
ideal and coincide in Radon metric groups.
This result extends main results established in [6], [13], [20]. For a
Borel probability measure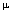 
in a Polish group G, we construct the
generator
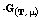of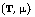 
shy sets which is quasi-finite, whenever the
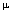is a 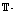quasi-generator. Using Okazaki-Takahashi
result [23], we prove that, if a group of admissible translations (in
the sense of quasi-invariance) for a Borel probability 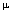in a Polish topological vector space
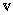is thick, then the generator
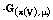of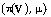 
shy (equivalently, shy) sets is quasi-finite.
For such a Borel measure 
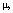we construct a quasi-finite semi-finite
translation-invariant Borel measure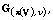 
which is equivalent to the generator
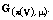Also, we show that Okazaki’s
dichotomy [22] is not valid for generators of 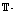shy sets in 
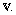By using technique of 
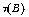cm and 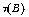shy sets, we solve negatively a certain
problem posed by Fremlin in [9].
generator of shy sets, Haar null set, shy set, Polish topological vector space.
