Volume no :5, Issue no: 1, May 2010

Journal of Mathematical Sciences: Advances and Applications

ASYMPTOTIC BEHAVIOR OF RELAXED DIRICHLET PROBLEMS RELATED TO HOMOGENEOUS STRONGLY LOCAL FORMS

Author's: Marco Biroli and Silvana Marchi
Pages: [39] - [83]
Received Date: March 9, 2010
Submitted by:

Abstract

We study the asymptotic behavior of the solutions to a relaxed Dirichlet problem associated with p-homogeneous strongly local forms, 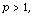having a local 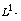density and to measures 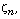which do not charge sets of zero capacity. We prove that there exists a subsequence of 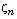that 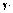converges to a measure 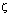of the same type, and we also prove the convergence of the relative solutions in

Keywords

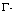
nonlinear Dirichlet forms, relaxed Dirichlet problems, 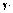convergence.