Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: I. M. Proudnikov
Pages: [227] - [244]
Received Date: April 1, 2009; Revised June 7, 2009
Submitted by: Zeyad Abdel Aziz Mah’d Al Zhour.
It is proved that matrices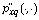 
of the second mixed derivatives of the
support function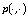 
for an introduced set-valued mapping
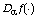for Lipschitz function 
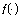exist almost everywhere in 
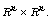Matrices 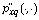are similar to matrices of second
derivatives for smooth functions. The Clarke subdifferential of the
set-valued mapping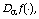 
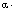generalized and their continuous extension
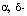generalized matrices for 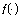were defined. Under some assumption, a
continuous extension of the Clarke, subdifferential and the form of
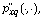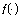when is twice continuous differentiable were
found. An optimization method is proposed for using these matrices in
nonsmooth optimization.
Lipschitz functions, Lipschitz set-valued mappings, support function, generalized matrices for Lipschitz functions, Clarke subdifferential for set-valued mappings, Newton’s optimization process.
