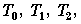Journal of Mathematical Sciences: Advances and Applications
URYSOHN, 
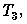AND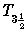 
ARE EQUIVALENT AND INFINITELY MANY NEW
CHARACTERIZATIONS OF THE 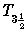PROPERTYAuthor's: Charles Dorsett
Pages: [73] - [89]
Received Date: February 17, 2017
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100121777
The ((completely regular) and 
) topological property, commonly denoted by
is a long-known, long-studied, useful
separation axiom. It is well-known that 
implies 
which implies Urysohn, which implies
which implies
which implies 
and examples are known showing the
implications are not reversible. Thus questions concerning topological
properties for which the six separation axioms are equivalent arise.
In this paper, a new category of topological properties is introduced
and used to give infinitely many topological properties for which the
six separation axioms are equivalent, and earlier results from the
study of weakly Po spaces and properties are used to give
infinitely many new characterizations of the separation axiom.
weakly P properties, completely regular, 
