Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Pedro Manuel Dominguez Wade
Pages: [29] - [46]
Received Date: October 29, 2015
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100121566
Let R be a ring of algebraic integers of an algebraic number
field F and let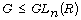 
be a finite group. In [11] was proved that
the R-span of G is just the matrix ring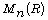 
of the 
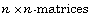over R if and only if the Brauer
reduction of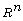 
modulo every prime is absolutely
irreducible. In this paper, we show that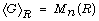 
if and only if the Brauer reduction of
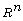modulo a finite number of primes is
absolutely irreducible. Moreover, we give conditions for n,
under which 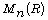is a Schur ring.
Schur ring,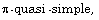 
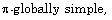G-weight, reduction modulo p,
reduction modulo 
