Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Ren Zongxiu, Wei Leilei and Liu Xiao
Pages: [277] - [286]
Received Date: December 7, 2008
Submitted by:
There are many non-linear developmental equations in the process of
modern physics research. The Sine-Gordon equation has become an
important model of the infinite-dimensional dynamical systems as it
has many interesting phenomena, for Sine-Gordon equation, because of
its conservation of energy, we lay too much stress on the numerical
schemes of conservation of energy in recent years, and which also have
a better result than ones of non-conservation, but the damped
Sine-Gordon equation is non-conservation of energy because of its
damping term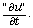 
An ADI finite element scheme and its error
estimation is studied in this paper, by using this method, a
multidimensional problem can be solved as a series of one dimensional
problems. With the help of thoery and skill of prior estimates of
differential equations optimal order error estimate is derived. At
last, we give the numerical results of the scheme.
the generalized nonlinear Sine-Gordon equation, ADI, finite element scheme, error estimates, convergence, stability.
