Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: H. Doostie and A. Sadeghieh
Pages: [245] - [256]
Received Date: November 10, 2008
Submitted by:
A semigroup S is called commuting regular if for all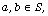 
there exists an element 
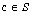such that 
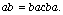This paper investigates all of the
non-abelian commuting regular inverse subsemigroups of the full
transformation semigroups 
and 
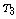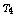and determines all of them up to
isomorphisms. Moreover, the notion of commutativity degree of a finite
group will be generalized for the semigroups and it will be calculated
for the studied subsemigroups. This study gives a necessary and
sufficient condition for a commuting regular inverse semigroup to be a
group.
commuting regularity, transformation semigroups, inverse semigroup, completely regular semigroups.
