Volume no :2, Issue no: 2, May 2009

Journal of Mathematical Sciences: Advances and Applications

A COMPLETE QUASI-ANTIORDER IS THE INTERSECTION OF A COLLECTION OF QUASI-ANTIORDERS

Author's: Daniel Abraham Romano
Pages: [215] - [220]
Received Date: December 15, 2008
Submitted by:

Abstract

Setting of this paper is Bishop\'s constructive mathematics. For a relation 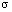on a set with apartness is called quasi-antiorder if it is consistent and cotransitive. The quasi-antiorder 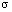is complete if holds 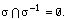In this paper the following assertion ‘A quasi-antiorder is the intersection of a collection of quasi-antiorders.’ is given.

Keywords

constructive mathematics, set with apartness, anti-order, quasi-antiorder.