Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Luming Shen and Xinqiang Li
Pages: [37] - [43]
Received Date: April 19, 2015
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100121491
For any irrational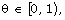 
let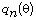 
be n-th continuant of 
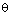in its continued fraction expansion.
Davenport and Roth showed that if 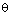satisfies
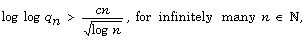
for all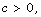 
then 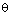must be transcendental. We call a set
A purely transcendental set, if all the elements in A
are transcendental. In this note, we intend to explain that if a
purely transcendental set is determined merely by the properties of
the individual continuants, besides algebraic numbers, most
transcendental numbers are excluded from this set. Namely, let
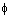be a positive function defined on
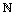and set
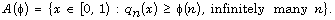
If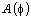 
is a purely transcendental set, then the
set 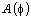is of Hausdorff dimension at most one-half.
transcendental numbers, continued fractions, Hausdorff dimension.
