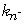Volume no :2, Issue no: 1, February 2009

Journal of Mathematical Sciences: Advances and Applications

VISCOSITY APPROXIMATION TO COMMON FIXED POINTS OF LIPSCHITZIAN NONEXPANSIVE MAPPINGS IN BANACH SPACES

Author's: Hongliang Zuo and Min Yang
Pages: [121] - [135]
Received Date: September 8, 2008
Submitted by:

Abstract

Let E be a real Banach space with uniformly Gâteaux differentiable norm possessing uniform normal structure. K is a nonempty bounded closed convex subset of E, and 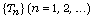is a sequence of 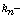Lipschitzian nonexpansive mappings from K into itself such that 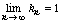and 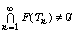and f be a contraction on K. Under sutiable conditions on sequence 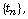we show the sequence 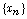defined as 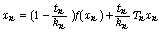exists and converges strongly to a fixed point of a mapping T. 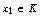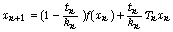And we apply it to prove the iterative process defined by and converges strongly to the same point.

Keywords

uniformly Gâteaux differentiable norm, uniform normal structure, viscosity approximation methods, Lipschitzian mappings.