Volume no :31, Issue no: 1, January

Journal of Mathematical Sciences: Advances and Applications

ON THE TAYLOR COEFFICIENTS OF BLASCHKE AND DJRBASHYAN PRODUCTS AND THEIR CONNECTING FUNCTIONS

Author's: Rubik Dallakyan and Ishkhan Hovhannisyan
Pages: [69] - [82]
Received Date: January 18, 2015
Submitted by:
DOI: http://dx.doi.org/10.18642/jmsaa_7100121444

Abstract

Using the Riemann-Liouville integration-differentiation operator, Djrbashyan generalized the class of Nevanlinna’s meromorphic functions in the unit circle including the product 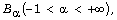which in the special case of 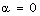coincide with the Blaschke product. Furthermore, when Djrbashyan and Zakaryan showed a connection between the products 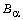and B of Blaschke.

In this work, we show the existence of Blaschke and Djrbashyan products with the same null sets, Taylor-Maclaurin coefficients satisfying certain new constraints. To achieve that result, we use a theorem of Shapiro and Shields and a remark from Zakaryan. We further estimate the Taylor coefficients of these functions.

Keywords

Riemann-Liouville integration-differentiation operator, Blaschke product, Djrbashyan product, Djrbashyan kernels, Dirichlet-type classes.