Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: E. O. Ifidon
Pages: [663] - [677]
Received Date: June 30, 2008
Submitted by:
Consider the fully nonlinear parabolic problem
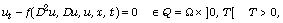
where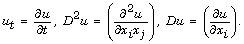 
is a bounded open set in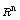 
and 
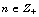is a positive integer. It is well known that
the classical theory for viscosity solutions does not cover the case
where f is discontinuous. This is because the straight forward
method of comparing sub and super solutions does not work if f
is discontinuous with respect to x and t. In order
therefore, to obtain existence and uniqueness results for this class
of problems, there is a need to introduce the concept of generalized
viscosity solutions where the components of the equations are elements
of the space of generalized functions. This is achieved using
nonstandard methods involving classical estimates. No linearization of
f is assumed. We show that our solutions are consistent with
the distributional solutions whenever they exist.
solution, nonlinear parabolic equations.
