Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Lan Yan and Peng Xiangyang
Pages: [533] - [546]
Received Date: May 14, 2008
Submitted by:
An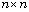 
real P is said to be an
anti-symmetric orthogonal matrix if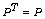 
and 
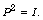An 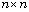real X is said to be an
anti-symmetric orthogonal anti-symmetric matrix with respect to the
symmetric orthogonal-matrix P if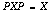 
and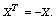 
By applying the generalized singular value
decomposition (GSVD) of matrices, this paper provides the necessary
and sufficient conditions for the existence and the expression for the
anti-symmetric orthogonal anti-symmetric with a symmetric orthogonal
matrix P solutions of the matrix equation 
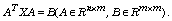In addition, in solution set of the
equation, the expression of the optimal approximation solution to the
given matrix and of least-norm solution are derived.
matrix equation, symmetric orthogonal anti-symmetric matrices, optimal approximation, least-norm solution.
