Volume no :1, Issue no: 2, August 2008

Journal of Mathematical Sciences: Advances and Applications

A REMARK ON THE PRODUCTS OF DISTRIBUTIONS AND SEMIGROUPS

Author's: ADEM KILIÇMAN
Pages: [423] - [430]
Received Date: July 13, 2008
Submitted by:

Abstract

In this study we consider 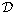the space of infinitely differentiable functions with compact support and 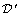the space of distributions defined on 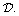Now let 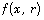be distribution in 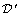and let 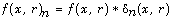where 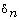is a certain sequence which converges to the Dirac-delta function. Then the products 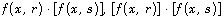are defined as the limit of the sequences 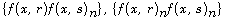provided that the limits 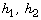exist in the sense of





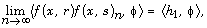
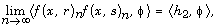
respectively, for all [top=3[img=admin/img_data//722/equation/image5617.gif] in 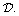In general, two products do not necessarily be equal. In this work, it is proved that two products are equal if they satisfy a property which we call semigroup condition. It is also proved that if products satisfy the semigroup condition then hold the associativity.

Keywords

distributions, delta-function, regular sequence, product of distributions, semigroup.