Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Rabah Kellil
Pages: [29] - [39]
Received Date: December 4, 2013; Revised January 16, 2014
Submitted by:
In this paper, we introduce the notions of a left almost semiring
(LA-semiring) and a strong left almost semiring (strong LA-semiring)
and then the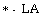 
semirings. We prove that many results
obtained for semirings still valid in our case. We establish a
relationship between the idempotents for both the addition and the
multiplication. We prove in the case of strong LA-semiring, that the
set of multiplicative idempotent;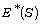 
is closed under the multiplication and so
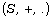is an orthodox strong LA-semiring. [5],
[3], [4], [7], and [8] can be used as a background for the subject.
An analogue to Theorem 2.8 in [7] or more precisely in what cases can
the multiplicative structure of a strong left almost semiring be a
product of almost groups (groups without the associativity) will be
studied in a forecoming paper?
semiring, regular semigroups, inverse semigroups, idempotents, orthodox semiring, medial law, left invertive law, left almost semiring.
