Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Ruma Kareem K. Ajeena and Hailiza Kamarulhaili
Pages: [43] - [56]
Received Date: November 30, 2013
Submitted by:
In this paper, we developed a method for accelerating multiplication
operation on classes of elliptic curve that are efficiently-computable
based on the GLV method of Gallant, Lambert and Vanstone that was
initially proposed in the year 2001, which uses a fast endomorphisms
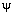with minimal polynomial 
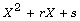to compute the multiple 
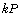of a point P of order n lying
on an elliptic curve. In the GLV method, the value k is
decomposed into the values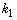 
and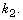 
Both values are expected to be bounded by
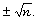However, when both values, or one of the
values is not within the range, then, in the GLV method, one needs to
choose a new k and obtain a new generator to generate a new
decomposition values that fall within the range. Even so, this new
chosen k does not guarantee the decomposition values would fall
within the range. Finding k with decomposition values that fall
within the range will usually acquires big loops and more computation
complexity. In this work, we propose a new method called the integer
sub-decomposition (ISD) to complement the GLV method and to overcome
this problem. In addition, this paper highlighted the computation
complexity of ISD method that is obtained by computing the cost of
elliptic curve and finite field operations of all algorithms that
assemble the whole process. This result is then compared to the GLV
method in one cycle operation. Finally, from our experimental results,
it appears that the ISD method has helped to increase the successful
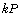computation percentage of in comparison with the GLV method. This
improvement has a direct impact on the scalar multiplication
techniques in elliptic curve cryptography, and will promote and help
to maintain the implementation of the elliptic curve cryptosystem in
the future.
elliptic curve cryptosystem, scalar multiplication, integer sub-decomposition, efficiently computable endomorphisms.
