Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: Glória Cravo
Pages: [69] - [90]
Received Date: April 14, 2008
Submitted by:
Matrix Completion Problems are an important branch of research on
Matrix Theory. In the last decades, many authors have studied this
type of questions. In this paper we mention the most important results
available in the literature, concerning the prescription of the
characteristic polynomial of a square matrix partitioned into
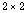blocks, when some of its blocks are fixed
and the others vary. We still present our contribution in this area.
In general, the solution of this type of problems contemplates
necessary and sufficient conditions with an expected form (involving
the interlacing inequalities for the invariant factors). However, in a
particular case, we show that the “expected” condition is not
necessary. For that purpose let us consider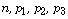 
be positive integers such that 
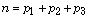and let 
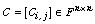be a partitioned matrix, where the blocks
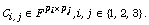Let f be a monic polynomial of degree
n and suppose that the blocks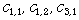 
are prescribed and the others are free. Let
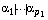be the invariant factors of the matrix
pencil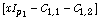 
and let 
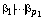be the invariant factors of
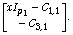
In this paper we show that the following divisibility condition
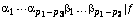
is not a necessary condition for the existence of a matrix C
with prescribed form and prescribed characteristic polynomial
f.
eigenvalues, inverse problems, matrix completion problems.
