Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: M. M. KHADER and A. S. HENDY
Pages: [1] - [39]
Received Date: July 12, 2013
Submitted by:
Fractional calculus had shown to be adequate models for various areas
of engineering, science, finance, applied mathematics,
bio-engineering, and others. However, many researchers remain unaware
of this field. In this paper, we deal with finding an analytical
criterion to determine the existence or non-existence of a numerical
solution for a system of fractional ordinary differential equations,
which is able to be reduced to a system of ordinary differential
equations with integer derivatives in terms of exp-function method,
which was first proposed by He and Wu under the space of functions
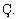The fractional derivative is described in
the Riemann-Liouville sense.
Our study will go across some stages. The first stage, we present how
to reduce a system of fractional ordinary differential equations to a
system of ordinary differential equations with integer derivatives by
using the properties of class 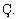The second stage, we introduce a theorem
and its proof, which gives an operator method to express the solution
of a system of ordinary differential equations as a generalization of
Navickas work in this field. The final stage, we present an algorithm,
which is used to clarify a criterion to express the solution of
fractional differential equation under the space 
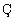in terms of exponential functions, and we
give three examples of systems of fractional differential equations in
which two of them are linear and the third is non-linear to be solved
by using our proposed technique.
multiplicative operator, operator method for ordinary differential equations, rank of Hankel matrices, exp-function method, system of fractional differential equations.
