Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: ALIREZA BEHTASH
Pages: [13] - [33]
Received Date: August 15, 2012; Revised November 13, 2012
Submitted by:
Here, we prove a theorem for Legendre transformation of some specific
derivative-like sequence chosen as the argument of Legendre transform
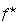of a function f using theory of
convex functions, mean value theorem in one dimensional Euclidean
space, and finally, a mathematical program established to provide some
conditions of local convexity that may be incompatible with the
existence of Legendre transformation. We also discuss the useful
results of this theorem along with numerous examples. These results
aim at providing a new set of Legendre transformations generated by a
given convex function, where the variable of the function is regarded
as an interval length. This generation is actually based on an
appropriate modification of variables, which yields the treatment of
Legendre transformations over a specific field of distributions.
Legendre transformation, local convexity, quasiconvexity, pseudomean value.
