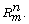Journal of Mathematical Sciences: Advances and ApplicationsAuthor's: ALI H. HAKAMI
Pages: [39] - [52]
Received Date: September 12, 2012
Submitted by:
Let m be a positive integer. Denote to the ring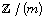 
by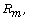 
and a Cartesian product of n copies
of 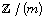by 
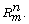Let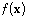 
be a quadratic polynomial in 
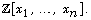Writ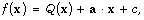e 
where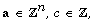 
and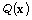 
is a quadratic form given by 
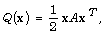where A is a symmetric 
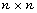matrix with integer entries. Assume
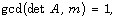unless we mention else. Let V be
the set of points in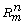 
satisfying the congruence 
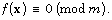If 
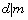and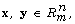 
we shall say 
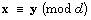if x is congruent to y
modulo the ideal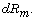 
For any subset S of 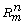and divisor d of m, let
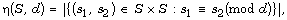where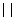 
denote to the cardinality. Let 
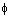denote the Euler phi-function, 
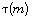denote the number of distinct positive
divisors of m, and for positive integers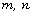 
set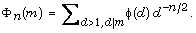 
In this paper, we shall prove that for any
subsets S and T of 
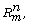with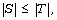 
we have
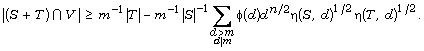
We also show that the above result can be made more precise when
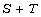is a box of points in
