[1] J. S. Ahn and P. Danzig, Packet: network simulation: Speedup and
accuracy versus timing granularity, IEEE/ACM Transactions on
Networking 4(5) (1996), 743-757.
[2] H. J. Alme, G. Rodrigue and G. Zimmerman, Domain decomposition for
parallel Laser-Tissue Models with Monte Carlo Transport, Niederreiter,
H. Spanier, J. eds., Monte Carlo and Quasi Monte Carlo Methods, pp.
86-97, Springer, 1998.
[3] A. D. Al-Nasser, L-Ranked set sampling: A generation
procedure for robust visual sampling, Communications in Statistics:
Simulation and Computation 36(1) (2007), 33-43.
[4] E. C. Anderson, Monte Carlo Methods for Inference in Population
Genetic Models, 2001.
[5] A. N. Avramidis and P. L’Ecuyer, Efficient Monte Carlo and
quasi-Monte Carlo option pricing under the variance-gamma model,
Management Science 52(12) (2006), 1930-1944.
[6] J. Banks, J. S. Carson, B. L. Nelson and D. M. Nicol, Discrete-
Event System Simulation (3rd edition), Upper Saddle River, New Jersey,
Prentice Hall, 2001.
[7] V. D. Barnett, Random Negative Exponential Deviates 2-Pair-Wise
Correlated Sets of 10,000 Observations: With Facilities for the
Generation of Random 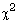 Deviates on Any Integral Number of Degrees
of Freedom, Cambridge University Press, New York, 2005.
Deviates on Any Integral Number of Degrees
of Freedom, Cambridge University Press, New York, 2005.
[8] P. Bratley, B. L. Fox and L. E. Schrage, A Guide to Simulation
(2nd edition), Springer-Verlag, New York, 1987.
[9] M. E. Brenner, Selective sampling-a technique for reducing sample
size in simulations of decision making problems, Journal of Industrial
Engineering 14 (1963), 291-296.
[10] R. M. Butler and E. L. Lusk, Monitors, message and clusters: The
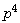 parallel programming system, Parallel
Computing 20(4) (1994), 547-564.
parallel programming system, Parallel
Computing 20(4) (1994), 547-564.
[11] R. C. H. Cheng, The use of antithetic control variates in
computer simulations, Winter Simulation Conference, Proceedings of the
13th conference on winter simulation, IEEE press, 1981.
[12] J. Chergui and P. F. Lavallée, Open MP Parallélisation
multi tâches pour machines à mémoire partagée, Institut du
developpement et des ressources en Informatique scientifique, 2006.
[13] R. Davidson and J. G. Mac Kinnon, Regression-based methods for
using control and antithetic variates in Monte Carlo simulation,
Journal of Econometrics 54 (1992), 203-222.
[14] T. R. Dell and J. L. Clutter, Ranked set sampling theory with
order statistics background, Biometrics 28 (1972), 545-555.
[15] A. Doucet, N. de Freitas and N. Gordon, Sequential Monte Carlo
Methods in Practice, Springer Verlag, 2001.
[16] S. Drew and T. Homen de Mello, Some large deviations results for
latin hypercube sampling, Winter Simulation Conference, M. E. Kuhl, N.
M. Steiger, F. B. Armstrong and J. A. Joines, eds., 2005.
[17] R. Duncan, A survey of parallel computer architectures, Computer
23(2) (1990), 5-16.
[18] S. Ehrenfeld and S. Ben Tuvia, The efficiency of statistical
simulation procedures, Technometrics 4 (1962), 257-275.
[19] G. S. Fishman, Monte-Carlo: Concepts, Algorithms and
Applications, Springer-Verlag, 1997.
[20] Flynn, Very high speed computing systems, Proceeding IEEE 54(12)
(1966), 1901-1909.
[21] A. Gest, A. Beguelin, J. Dongarra, W. Jiang, R. Manchek and V.
Sunderam, PVM: Parallel Virtual Machine, a user guide and tutorial for
network, Parallel Computing, The MIT press, 1994.
[22] L. K. Halls and T. R. Dell, Trial of ranked set sampling for
forage yiels, Forest Science 12 (1966), 22-26.
[23] J. M. Hammersley and K. W. Morton, A new Monte Carlo technique:
Antithetic variates, Proc. Cambridge Philos. Soc. 52 (1956),
449-475.
[24] N. Hoshino and A. Takemura, On reduction of finite sample
variance by extended Latin hypercube sampling, Bernoulli 6(6) (2000),
1035-1050.
[25] M. G. Kendall and S. Babington, Randomness and random sampling
numbers, J. Roy. Stat. Soc. 101 (1938), 147-166.
[26] J. P. C. Kleijnen, Design and analysis of simulations: Practical
statistical techniques, Simulation 28 (1977), 81-90.
[27] C. Kwon and J. D. Tew, Strategies for combining antithetic
variates and control variates in designed simulation experiments,
Management science 40(8) 1994.
[28] A. M. Law and W. D. Kelton, Simulation Modeling and Analysis (3rd
ed.), McGraw-Hill, New-York, 2000.
[29] P. L’Ecuyer, Quasi Monte Carlo methods for simulation,
Winter Simulation Conference, S. Chick, P. J. Sanchez, D. Ferrin and
D. J. Morrice, eds., 2003.
[30] P. L’Ecuyer, C. Lécot and B. Tuffin, Randomized
Quasi-Monte Carlo Simulation of Markov Chains with an Ordered State
Space, H. Niederreiter and D. Talay, eds., Monte Carlo and Quasi-Monte
Carlo Methods 2004, Springer-Verlag, 2006.
[31] P. L’Ecuyer and E. Buist, Variance reduction in the
simulation of call centers, L. F. Perrone, F. P. Wieland, J. Liu, B.
G. Lawson, D. M. Nicol and R. M. Fujimoto, eds., Proceedings of the
2006 Winter Simulation Conference, 2006.
[32] Y. B. Lin, Parallel independent replicated simulation on networks
of workstations, Proceedings of the 8th Workshop on Parallel and
Distributed Simulation, ed., I. C. S. Press, 1994.
[33] W. L. Loh, On Latin hypercube sampling, The Annals of Statistics
24 (1996), 2058-2080.
[34] G. A. McIntyre, A method for unbiased selective sampling using
ranked sets, Aust. J. Agri. Res. 3 (1952), 385-390.
[35] M. D. McKay, R. J. Beckman and W. J. Conover, A comparison of
three methods for selecting values of input variables in the analysis
of output from a computer code, Technometrics 21 (1979), 239-245.
[36] W. J. Morokoff and R. E. Caflisch, Quasi random sequences and
their discrepancies, SIAM J. Sci. Comput. Dec: (1994), 1571-1599.
[37] H. A. Muttlak, Parameters estimation in a simple linear
regression using rank set sampling, Biometrical Journal 37(7) (2007),
799-810.
[38] B. L. Nelson and B. W. Schmeiser, Decomposition of some well
known variance reduction technique, J. Stat. Comput. Simul. 23(3)
(1986), 183-209.
[39] H. Niederreiter, Random number generation and quasi Monte-Carlo
methods, Philadelphia: CBMS-SIAM 63, 1992.
[40] G. Okten, A probabilistic result on the discrepancy of a
hybrid-Monte Carlo sequence and applications, Monte Carlo Methods and
Applications 2(4) (1996), 255-270.
[41] G. Okten and A. Srinivasan, Parallel Quasi-Monte Carlo
Applications on a Heterogeneous Cluster, K. T. Fang, F. J. Hickernell
and H. Niederreiter, eds., Monte Carlo and Quasi- Monte Carlo Methods,
Springer-Verlag, 2002.
[42] G. Okten, B. Tuffin and V. Bugaro, A central limit theorem and
improved error bounds for a hybrid-Monte Carlo sequence with
applications in computational finance, Journal of Complexity 22(4)
(2006), 435-458.
[43] A. B. Owen, A central limit theorem for Latin hypercube sampling,
J. Roy. Statist. Soc. Ser. B 54 (1992), 541-551.
[44] A. B. Owen, Monte Carlo variance of scrambled net quadrature,
SIAM J. Numer. Anal. 34 (5) (1997), 1884-1910.
[45] M. Pidd, Computer Simulation in Management Science (4th ed.),
Chichester: John Wiley and Sons, 1998.
[46] R. Robinson, Simulation: The practice of Model Development and
Use, Chichester: John Wiley and Sons, 2004.
[47] C. P. Robert and G. Casella, Monte Carlo Statistical Methods (2nd
ed.), Springer Science+Business Media Inc., 2004.
[48] K. W. Ross, D. Tsang and J. Wang, Monte-Carlo summation and
integration applied to multichain queueing networks, J. Assoc. Comput.
Mach. 41(6) (1994), 1110-1135.
[49] S. M. Ross, Simulation, 2nd ed., Academic Press, New York,
1997.
[50] R. Y. Rubinstein, Simulation and the Monte Carlo Method, Wiley,
New York, 1981.
[51] E. Saliby, Understanding the variability of simulation results:
An empirical study, J. Oper. Res. Soc. 41(4) (1990), 319-327.
[52] E. Saliby, Descriptive Sampling: A better approach to Monte Carlo
simulation, J. Oper. Res. Soc. 41(12) (1990), 1133-1142.
[53] E. Saliby and R. J. Paul, Implementing descriptive sampling in
three phase discrete event simulation models, J. Oper. Res. Soc. 44
(1993), 147-160.
[54] E. Saliby, Descriptive sampling: an improvement over Latin
hypercube sampling, Winter Simulation Conference (1997), 230-233.
[55] E. Saliby and F. Pacheco, An empirical evaluation of sampling
methods in risk analysis simulation: Quasi Monte Carlo, Descriptive
Sampling, and Latin Hypercube sampling, Winter Simulation Conference
(2002), 1606-1610.
[56] R. E. Shannon, Systems Simulation the Art and Science,
Prentice-Hall, New-Jersey, 1975.
[57] D. B. Skililcorn, A taxonomy for computer architectures, IEEE
Computer 21(11) (1985), 46-57.
[58] I. H. Sloan and S. Joe, Lattice Methods for Multiple Integration
Clarendon Press, Oxford, 1994.
[59] M. Stein, Large sample properties of simulations using Latin
hypercube sampling, Technometrics 29 (1987), 143-151.
[60] T. Ken Seng and P. P. Boyle, Applications of randomized low
discrepancy sequences to the valuation of complex securities, J.
Econom. Dynam. Control 24(11-12) (2000), 1747-1782.
[61] M. Tari and A. Dahmani, The three phase discrete event simulation
using some sampling methods, IJAMAS 3D 05 (2005), 37-48.
[62] M. Tari and A. Dahmani, The refining of descriptive sampling,
IJAMAS 3M05 (2005), 41-68.
[63] M. Tari and A. Dahmani, Flowshop simulator using different
sampling methods, Operational Research: An International Journal 5
(2005), 261-272.
[64] M. Tari and A. Dahmani, Refined descriptive sampling: A better
alternative to Monte Carlo simulation, Simulation Modelling Practice
and theory 14 (2006), 143-160.
[65] S. J. E. Taylor, V. Hlupic, S. Robinson and J. Ladbrook,
GroupSim: Investigating issues in collaborative simulation modeling,
Oper. Res. Soc. Simul. (2002), 11-18.
[66] K. D. Tocher, The Art of Simulation, English University Press,
London, 1963.
[67] B. Tuffin, Variance reductions applied to productform multi-class
queueing networks, ACM Trans. Modeling and Computer Simulation 7(4)
(1997), 478-500.
[68] B. Tuffin and L. M. Le Ny, Parallélisation d’une
combinaison des méthodes de Monte-Carlo et quasi Monte-Carlo et
application aux réseaux de files d’attente, RAIRO Operations
Research 34 (2000), 85-98.
[69] MPI Forum: April MPI (A Message Passing Interface Standard),
1994.