[1] M. Alizadeh, G. M. Cordeiro, E. de Brito and C. G. B. Demetrio,
The beta Marshall-Olkin family of distributions, Journal of
Statistical Distributions and Applications 2(4) (2015), 1-18.
DOI: https://doi.org/10.1186/s40488-015-0027-7
[2] A. Alzaatreh, C. Lee and F. Famoye, A new method for generating
families of continuous distributions, Metron 71(1) (2013), 63-79.
DOI: https://doi.org/10.1007/s40300-013-0007-y
[3] A. Alzaghal, F. Famoye and C. Lee, Exponentiated 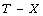 family of distributions with some applications,
International Journal of Statistics and Probability 2(3) (2013),
31-49.
family of distributions with some applications,
International Journal of Statistics and Probability 2(3) (2013),
31-49.
DOI: https://doi.org/10.5539/ijsp.v2n3p31
[4] S. K. Ashour and W. M. Afify, Estimation of the parameters of
exponentiated Weibull family with type Ii progressive interval
censoring with random removals, Journal of Applied Sciences Research
4(11) (2008), 1428-1442.
[5] W. Barreto-Souza, A. H. S. Santos and G. M. Cordeiro, The beta
generalized exponential distribution, Journal of Statistical
Computation and Simulation 80(2) (2010), 159-172.
DOI: https://doi.org/10.1080/00949650802552402
[6] M. Bourguignon, R. B. Silva and G. M. Cordeiro, The
Weibull-G family of probability distributions, Journal of Data
Science 12(1) (2014), 5-68.
[7] A. Choudhury, A simple derivation of moments of the exponentiated
Weibull distribution, Metrika 62(1) (2005), 17-22.
DOI: https://doi.org/10.1007/s001840400351
[8] G. M. Cordeiro and M. de Castro, A new family of generalized
distributions, Journal of Statistical Computation and Simulation 81(7)
(2011), 883-898.
DOI: https://doi.org/10.1080/00949650903530745
[9] G. M. Cordeiro, C. T. Cristino, E. M. Hashimoto and E. M. M.
Ortega, The beta generalized Rayleigh distribution with applications
to lifetime data, Statistical Papers 54(1) (2013), 133-161.
DOI: https://doi.org/10.1007/s00362-011-0415-0
[10] M. A. T. Elshahat, Approximate Bayes Estimators for the
Exponentiated Weibull Parameters with Progressive Internal Censoring,
The 20th Annual Conference on Statistics and Modeling in Human and
Social Science, Faculty of Economic and Political Science, Cairo
University, Egypt (2008), 123-136.
[11] F. Famoye, C. Lee and O. Olumolade, The beta Weibull
distribution, Journal of Statistical Theory and Applications 4 (2005),
121-136.
[12] R. D. Gupta and D. Kundu, Exponentiated exponential family: An
alternative to gamma and Weibull Distributions, Biometrical Journal
43(1) (2001), 117-130.
DOI:
https://doi.org/10.1002/1521-4036(200102)43:1<117::AID-BIMJ117>3.0.CO;
2-R
[13] H. M. Salem and M. A. Selim, The generalized Weibull-exponential
distribution: Properties and applications, International Journal of
Statistics and Applications 4(2) (2014), 102-112.
DOI: https://doi.org/10.5923/j.statistics.20140402.04
[14] Laba Handique and Subrata Chakraborty, Beta generated
Kumaraswamy-G and other new families of distribution, arXiv
preprint arXiv:1603.00634 (2016), 1-34.
[15] J. F. Kenney and E. S. Keeping, Mathematics of Statistics,
101-102, Part 1, 3rd Edition, Princeton, NJ, 1962.
[16] C. Kim, J. Jung and Y. Chung, Bayesian estimation for the
exponentiated Weibull model type II progressive censoring, Statistical
Papers 52(1) (2011), 53-70.
DOI: https://doi.org/10.1007/s00362-009-0203-2
[17] C. Lee, F. Famoye and O. Olumolade, Beta-Weibull distribution:
Some properties and applications to censored data, Journal of Modern
Applied Statistical Methods 6(1) (2007), 173-186.
DOI: https://doi.org/10.22237/jmasm/1177992960
[18] M. A. W. Mahmoud and M. G. M. Ghazal, Estimations from the
exponentiated Rayleigh distribution based on generalized type-II
hybrid censored data, Journal of Egyptian Mathematical Society 25(1)
(2017), 71-78.
DOI: https://doi.org/10.1016/j.joems.2016.06.008
[19] E. Mahmoudi, The beta generalized Pareto distribution with
application to lifetime data, Mathematics and Computers in Simulation
81(11) (2011), 2414-2430.
DOI: https://doi.org/10.1016/j.matcom.2011.03.006
[20] A. L. Morais, G. M. Cordeiro and Audrey H. M. A. Cysneiros, The
beta generalized logistic distribution, Brazilian Journal of
Probability and Statistics 27(2) (2013), 185-200.
DOI: https://doi.org/10.1214/11-BJPS166
[21] J. J. A. Moors, A quantile alternative for kurtosis, Journal of
the Royal Statistical Society: Series D 37(1) (1988), 25-32.
DOI: http://dx.doi.org/10.2307/2348376
[22] S. Nadarajah and S. Kotz, The beta exponential distribution,
Reliability Engineering and System Safety 91(6) (2006), 689-697.
DOI: https://doi.org/10.1016/j.ress.2005.05.008
[23] M. M. Nassar and F. H. Eissa, On the exponentiated Weibull
distribution, Communications in Statistics-Theory and Methods 32(7)
(2003), 1317-1336.
DOI: https://doi.org/10.1081/STA-120021561
[24] M. M. Nassar and F. H. Eissa, Bayesian estimation for the
exponentiated Weibull model, Communications in Statistics-Theory and
Methods 33(10) (2005), 2343-2362.
DOI: https://doi.org/10.1081/STA-200031447
[25] P. E. Oguntunde, O. S. Balogun, H. I. Okagbue and S. A. Bishop,
The Weibull-exponential distribution: Its properties and applications,
Journal of Applied Sciences 15(11) (2015), 1305-1311.
DOI: https://doi.org/10.3923/jas.2015.1305.1311
[26] O. C. Okoli, G. A. Osuji, D. F. Nwosu and K. N. C. Njoku, On the
modified extended generalized exponential distribution, European
Journal of Statistics and Probability 4(4) (2016), 1-11.
[27] A. K. Olapade, On extended generalized exponential distribution,
British Journal of Mathematics and Computer Science 4(9) (2014),
1280-1289.
DOI: https://doi.org/10.9734/BJMCS/2014/8191
[28] M. Pal, M. M. Ali and J. Woo, Exponentiated Weibull distribution,
Statistica 66(2) (2006), 139-147.
DOI: https://doi.org/10.6092/issn.1973-2201/493
[29] R. R. Pescim, C. G. B. Demétrio, G. M. Cordeiro, E. M. M.
Ortega and M. R. Urbano, The beta generalized half-normal
distribution, Computation Statistics and Data Analysis 54(4) (2010),
945-957.
DOI: https://doi.org/10.1016/j.csda.2009.10.007
[30] A. M. Salem and O. E. Abo-Kasem, Estimation for the parameters of
the exponentiated Weibull distribution based on progressive hybrid
censored samples, International Journal of Contemporary Mathematical
Sciences 6(35) (2011), 1713-1724.
[31] R. L. Smith and J. C. Naylor, A comparison of maximum likelihood
and Bayesian estimators for the three-parameter Weibull distribution,
Journal of the Royal Statistical Society: Series C 36(3) (1987),
358-369.
DOI: https://doi.org/10.2307/2347795
[32] N. Singla, K. Jain and S. K. Sharma, The beta generalized Weibull
distribution: Properties and applications, Reliability Engineering
System Safety 102 (2012), 5-15.
DOI: https://doi.org/10.1016/j.ress.2012.02.003
[33] L. Zea, R. Silva, M. Bourguignon, A. Santos and M. Corderio, The
beta exponentiated Pareto distribution with application to bladder
cancer susceptibility, International Journal of Statistics and
Probability 1(2) (2012), 8-19.
DOI: https://doi.org/10.5539/ijsp.v1n2p8