Journal of Statistics: Advances in Theory and Applications[1] I. L. Amerise and A. Tarsitano, Correction methods for ties in
rank correlations, Journal of Applied Statistics 42(12) (2015),
2584-2596.
DOI: https://doi.org/10.1080/02664763.2015.1043870
[2] I. L. Amerise, M. Marozzi and A. Tarsitano, Pvrank: Rank
Correlations, R Package Version 1.1.2, 2016.
http://CRAN.R-project.org/package=pvrank
[3] A. Tarsitano and I. L. Amerise, Effectiveness of rank correlations
in curvilinear relationships, Behaviormetrika 44(2) (2017),
351-368.
DOI: https://doi.org/10.1007/s41237-017-0020-1
[4] A. D. Barbour and L. H. Y. Chen, The permutation distribution
matrix correlation statistics, In: A. D. Barbour and L. H. Y. Chen
(Editors), Stein‘s Method and Applications, Singapore University
Press (2005), 223-245.
[5] O. Chisini, Sul Concetto di Media, Periodico di Matematiche 9(2)
(1929), 106-116.
[6] D. M. Cifarelli, P. L. Conti and E. Regazzini, On the asymptotic
distribution of a general measure of monotone dependence, The Annals
of Statistics 24(3) (1996), 1386-1399.
DOI: https://doi.org/10.1214/aos/1032526975
[7] P. H. DuBois, Formulas and tables for rank correlation, The
Psychological Record 3 (1939), 46-56.
[8] R. A. Gideon and A. Hollister, A rank correlation coefficient
resistant to outliers, Journal of the American Statistical Association
82(398) (1987), 656-666.
[9] C. Gini, Sulla determinazione dell’indice di cograduazione,
Metron 13 (1939), 41-48.
[10] G. Girone, S. Montrone and D. Leogrande, La distribuzione
campionaria dell’indice di cograduazione di Gini per dimensioni
campionarie fino a 24, Annali del Dipartimento di Scienze Statistiche
“Carlo Cecchiâ€, Università degli Studi di Bari 24
(2010), 246-271.
[11] W. Hoeffding, A non-parametric test of independence, The Annals
of Mathematical Statistics 19(4) (1948), 546-557.
DOI: https://doi.org/10.1214/aoms/1177730150
[12] M. G. Kendall, The treatment of ties in ranking problems,
Biometrika 33(3) (1945), 239-251.
DOI: https://doi.org/10.1093/biomet/33.3.239
[13] W. Maciak, Exact null distribution for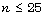 
and probability approximations for
Spearman’s score in an absence of ties, Journal of
Nonparametric Statistics 21(1) (2009), 113-133.
DOI: https://doi.org/10.1080/10485250802401038
[14] A. Mango, A distance function for ranked variables: A proposal
for a new rank correlation coefficient, Metodološski Zvezki 3(1)
(2006), 9-19.
[15] P. Muliere and G. Parmigiani, Utility and means in the 1930s,
Statistical Science 8(4) (1993), 421-432.
DOI: https://doi.org/10.1214/ss/1177010786
[16] E. B. Niven and C. V. Deutsch, Calculating a robust correlation
coefficient and quantifying its uncertainty, Computers & Geosciences
40 (2012), 1-9.
DOI: https://doi.org/10.1016/j.cageo.2011.06.021
[17] M. Panneton and P. Robillard, Algorithm AS 54: Kendall’s S
frequency distribution, Journal of the Royal Statistical Society,
Series C 21(3) (1972), 345-348.
DOI: https://doi.org/10.2307/2346291
[18] P. J. Rousseeuw and A. M. Leroy, Robust Regression and Outlier
Detection, John Wiley & Sons, New York, 1987.
[19] A. Tarsitano and R. Lombardo, A coefficient of correlation based
on ratios of ranks and anti-ranks, Jahrbucher für
Nationalökonomie und Statistik 233(2) (2013), 206-224.
DOI: https://doi.org/10.1515/jbnst-2013-0205
[20] A. Tarsitano and I. L. Amerise, On a new measure of rank-order
association, Journal of Statistical and Econometric Methods 4(2)
(2015), 1-4.
[21] L. Zhao, Z. Bai, C. C. Chao and W.-Q. Liang, Error bound in a
central limit theorem of double-indexed permutation statistics, The
Annals of Statistics 25(5) (1997), 2210-2227.
DOI: https://doi.org/10.1214/aos/1069362395
[22] Z. Zhang, Quotient correlation: A sample based alternative to
Pearson’s correlation, The Annals of Statistics 36(2) (2008),
1007-1030.
DOI: https://doi.org/10.1214/009053607000000866
