Journal of Statistics: Advances in Theory and Applications[1] F. J. Caro-Lopera, J. A. Díaz-García and G. González-Farías,
Noncentral elliptical configuration density, Journal of Multivariate
Analysis 101(1) (2010), 32-43.
DOI: https://doi.org/10.1016/j.jmva.2009.03.004
[2] F. J. Caro-Lopera, G. González-Farías and N. Balakrishnan, On
generalized Wishart distributions-I: Likelihood ratio test for
homogeneity of covariance matrices, Sankhyā: The Indian Journal of
Statistics, Series A 76(2) (2014), 179-194.
[3] F. J. Caro-Lopera, G. González-Farías and N. Balakrishnan,
Matrix-variate distribution theory under elliptical models-4: Joint
distribution of latent roots of covariance matrix and the largest and
smallest latent roots, Journal of Multivariate Analysis 145 (2016),
224-235.
DOI: https://doi.org/10.1016/j.jmva.2015.12.012
[4] Y. Chikuse, Asymptotic expansions for the joint and marginal
distributions of the latent roots of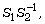 
Annals of the Institute of Statistical
Mathematics 29(2) (1977), 221-233.
[5] Y. Fujikoshi, Asymptotic expansions for the distributions of the
sample roots under nonnormality, Biometrika 67(1) (1980), 45-51.
DOI: https://doi.org/10.1093/biomet/67.1.45
[6] H. Hashiguchi, N. Takayama and A. Takemura, Distribution of the
ratio of two Wishart matrices and cumulative probability evaluation by
the holonomic gradient method, Journal of Multivariate Analysis 165
(2018), 270-278.
DOI: https://doi.org/10.1016/j.jmva.2018.01.002
[7] A. T. James, Distribution of matrix variates and latent roots
derived from normal samples, Annals of Mathematical Statistics 35(2)
(1964), 475-501.
[8] C. G. Khatri, On the exact finite series distribution of the
smallest or the largest root of matrices in three situations, Journal
of Multivariate Analysis 2(2) (1972), 201-207.
DOI: https://doi.org/10.1016/0047-259X(72)90027-9
[9] R. J. Muirhead, Aspects of Multivariate Statistical Theory,
John Wiley & Sons, New York, 1982.
[10] A. Shinozaki, H. Hashiguchi and T. Iwashita, Distribution of the
largest eigenvalue of an elliptical Wishart matrix and its simulation,
Journal of the Japanese Society of Computational Statistics 30(2)
(2018), 1-12.
DOI: https://doi.org/10.5183/jjscs.1708001_244
[11] N. Sugiura, Derivatives of the characteristic root of a synmetric
or a Hermitian matrix with two applications in multivariate analysis,
Communications in Statistics 1(5) (1973), 393-417.
DOI: https://doi.org/10.1080/03610927308827036
[12] N. Sugiura, Asymptotic expansion of the distributions of the
latent roots and the latent vector of the Wishart and multivariate
F matrices, Journal of Multivariate Analysis 6(4) (1976),
500-525.
DOI: https://doi.org/10.1016/0047-259X(76)90002-6
[13] T. Sugiyama, On the distribution of the largest latent root of
the covariance matrix, Annals of Mathematical Statistics 38(4) (1967),
1148-1151.
