Journal of Statistics: Advances in Theory and Applications
CLASS OF LIFE DISTRIBUTION[1] A. M. Abouammoh, R. Ahmad and A. Khalique, On new renewal better
than used classes of life distributions, Statist. Prob. Letters 48
(2000), 189-194.
[2] A. M. Abouammoh and A. Khalique, On tests of new renewal better
than used classes of life distributions, Parisankhyan Samikkha 5
(1998), 21-32.
[3] A. M. Abouammoh, S. A. Abdulghani and I. S. Qamber, On partial
orderings and testing of new better than renewal used classes,
Reliability Eng. Syst. Safety 43 (1994), 37-41.
[4] A. A. Abdel-Aziz, On testing exponentiality against RNBRUE
alternatives, Applied Mathematical Sciences 1(35) (2007),
1725-1736.
[5] S. E. Abu-Youssef, Amoment inequality on new renewal better than
used in expectation class of life distributions with hypothesis
testing application, International Journal of Reliability and
Applications 4 (2003), 191-199.
[6] S. E. Abu-Youssef, Moment inequality on new renewal better than
used class of life distributions with hypothesis testing application,
Applied Mathematics and Computation 149 (2004), 651-659.
[7] R. E. Barlow and F. Proschan, Statistical theory of reliability
and life testing, To begin with, Sliver Spring, MD. 13, (1981).
[8] M. C. Bhattacharjee, A. M. Abouammoh, A. N. Ahmed and A. M. Barry,
Preservation results for life distributions based on comparisons with
asymptotic remaining life under replacements, J. Appl. Probab. 37
(2000), 999-1009.
[9] J. V. Deshpande, S. C. Kochar and H. Singh, Aspects of positive
ageing, J. Appl. Probab. 23 (1986), 748-758.
[10] L. S. Diab, M. A. W. Mahmoud and S. M. EL-Arishy, A
non-parametric test of new renewal better than used class of life
distributions, Proceeding of International Conference on Mathematics
trends and developments, Cairo (EGYPT) 4 (2002), 191-203.
[11] L. S. Diab, M. A. W. Mahmoud and S. M. EL-Arishy, Testing renewal
new better than used life distributions based on U-test, Applied
Mathematical Modelling 29 (2005), 784-796.
[12] L. S. Diab, Non-parametric test of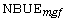 
class of life distributions, Journal of
Statistical Theory and Applications 8(3) (2009), 253-267.
[13] L. S. Diab, A new approach to moments inequalities for NRBU and
RNBU classes with hypothesis testing applications, International
Journal of Basic & Applied Sciences IJBAS-IJENS 13(06) (2013),
7-13.
[14] M. Franco, J. M. Ruiz and M. C. Ruiz, On closure of the IFR(2)
and NBU(2) classes, J. Appl. Probab. 38 (2001), 235-241.
[15] F. E. Grubbs, Fiducial bounds on reliability for the two
parameter negative exponential distribution, Technomet. 13 (1971),
873-876.
[16] E. L. Kaplan and P. Meier, Nonparametric estimation from
incomplete observation, J. Amer. Statist. Assoc. 53 (1958),
457-481.
[17] A. I. Kango, Testing for new is better than used, Communication
in Statistics Theor. Method. 12 (1993), 311-321.
[18] S. Kotz and N. L. Johnson, Encyclopedia of Statistical Sciences,
3, Wiley, New York, 1983.
[19] S. C. Kocher, Testing exponentiality against monotone failure
rate average, Comm. Statist. Theor. Meth. 14 (1985), 381-392.
[20] A. J. Lee, U-Statistics, Marcel Dekker, New York, 1989.
[21] X. Li, Z. Li and B. Jing, Some results about the NBUC class of
life distributions, Statist. Probab. Lett. 46 (2000), 229-237.
[22] M. A. W. Mahmoud, S. M. EL-Arishy and L. S. Diab, Moment
inequalities for testing new renewal better than used and renewal new
better than used classes of life distributions, International Journal
of Reliability and Applications 4(3) (2003), 97-123.
[23] A. Muller and D. Stoyan, Comparison Methods for Stochastic Models
and Risks, Wiley and Sons, New York, NY, 2002.
[24] A. R. Mugdadi and I. A. Ahmad, Moment inequalities derived from
comparing life with its equilibrium form, Journal of Statistical
Planning and Inference 134 (2005), 303-317.
[25] R. J. Pavur, R. L. Edgeman and R. C. Scott, Quadratic statistics
for the goodness of fit test of inverse Gaussian distribution, IEEE
Trans. Reli. 41 (1992), 118-123.
[26] A. E. Pena, Goodness of fit tests with censored data, (2002).
http://statmanStat.sc.edupenajtajkspresentedjtalkactronel
[27] E. J. G. Pitman, Some Basic Theory for Statistical Inference,
Chapman & Hall, London, 1979.
[28] S. M. Ross, Introduction to Probability Models, 8th Edition,
Academic Press, New York, NY, 2003.
[29] M. Shaked and J. G. Shanthikumar, Stochastic Orders and their
Applications, Academic Press, New York, NY, 1994.
[30] V. Susarla and J. Vanryzin, Empirical bayes estimations of a
survival function right censored observation, Ann. Statist. 6 (1978),
710-755.
