Journal of Statistics: Advances in Theory and Applications
SEMI-LATIN SQUARES[1] A. C. Atkinson and A. N. Donev, Optimum Experimental Designs,
Oxford University Press, New York, 1992.
[2] R. A. Bailey, Semi-Latin squares, J. Statist. Plann. and Inf. 18
(1988), 299-312.
[3] R. A. Bailey, Efficient semi-Latin squares, Statistica Sinica 2
(1992), 413-437.
[4] R. A. Bailey and P. E. Chigbu, Enumeration of semi-Latin squares,
Discrete Maths. 167/168 (1997), 73-84.
[5] R. A. Bailey and G. Royle, Optimal semi-Latin squares with side
six and block size two, Pro. Roy. Soc. Ser. A 453 (1997),
1903-1914.
[6] P. J. Cameron, P. Dobcsányi, J. P. Morgan and L. H. Soicher,
The external representation of block designs, Version 1.1 (2003).
http://designtheory.org
/library/extrep/ext-rep.pdf
[7] P. E. Chigbu, Block Designs: Efficiency Factors and Optimality
Criteria for Comparison, Linco Press Ltd., Enugu, Nigeria, 1998.
[8] P. E. Chigbu, Optimal semi-Latin squares for sixteen treatments in
blocks of size four, J. Nig. Statist. Assoc. 13 (1999), 11-25.
[9] P. E. Chigbu, The best of the three optimal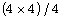 
semi-Latin squares, 
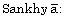The Indian J. Stats. 65(3) (2003),
641-648.
[10] P. E. Chigbu, A note on discriminating equally optimal semi-Latin
squares for sixteen treatments in blocks of size four, J. Nig.
Statist. Assoc. 17 (2004), 1-7.
[11] J. A. Fill and D. E. Fishkind, The Moore-Penrose generalized
inverse for sums of matrices, SIAM J. Matrix Anal. and Appl. 21(2)
(2000), 629-635.
[12] T. N. E. Greville, Some applications of the Pseudo inverse of a
matrix, SIAM Review 2(1) (1960), 15-22.
[13] I. B. Onukogu, Foundations of Optimal Exploration of Response
Surfaces, Ephrata Press, Nsukka, 1997.
[14] I. B. Onukogu and P. E. Chigbu (eds.), Super Convergent Line
Series in Optimal Design of Experiment and Mathematical Programming,
AP Express, Nsukka-Nigeria, 2002.
[15] L. Paterson, Circuits and efficiency in incomplete block designs,
Biometrika 70 (1983), 215-225.
[16] R. Penrose, A generalized inverse for matrices, Proc. Cambridge
Philos. Soc. 51 (1955), 406-413.
[17] R. J. Plemmons and R. E. Cline, The generalized inverse of a
nonnegative matrix, Proc. Amer. Mathcal. Soc. 31(1) (1972), 46-50.
[18] D. A. Preece and G. H. Freeman, Semi-Latin squares and related
designs, J. Roy. Statist. Soc. Ser. B 45(2) (1983), 267-277.
[19] D. Raghavarao, Construction and Combinatorial Problems in Design
of Experiments, Wiley, New York, 1971.
[20] M. A. Rakha, On the Moore-Penrose generalized inverse matrix,
Applied Math. and Computation 158 (2004), 185-200.
[21] S. R. Searle, Matrix Algebra Useful for Statistics, John Wiley &
Sons, Inc., Canada, 1982.
[22] N. P. Uto and P. E. Chigbu, On (M, S) and circuit
properties of the three optimal 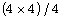semi-Latin squares, J. Math. Sci. 21(1)
(2010a), 43-52.
[23] N. P. Uto and P. E. Chigbu, A near-regular graph design approach
for ordering the three optimal 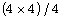semi-Latin squares, J. Nig. Stat. Assoc.
22 (2010b), 1-11.
[24] P. Wild, On circuits and optimality conjectures for block
designs, J. Roy. Stat. Soc. Ser. B 49(1) (1987), 90-94.
