Journal of Statistics: Advances in Theory and Applications[1] A. Belloni and V. Chernozhukov,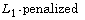 
quantile regression in high-dimensional
sparse models, Ann. Statist. 39 (2011), 82-130.
[2] P. K. Bhattacharya and P. L. Zhao, Semiparametric inference in a
partial linear model, Ann. Statist. 25 (1997), 244-262.
[3] K. Bollaerts, P. H. C. Eilers and A. Marc, Quantile regression
with monotonicity restrictions using P-splines and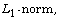 
Statistical Modelling 6 (2006), 189-207.
[4] R. J. Carroll, J. Fan, I. Gijbels and M. P. Wand, Generalized
partially linear single-index models, J. Amer. Statist. Assoc. 92
(1997), 477-489.
[5] C. H. Chen and K. C. Li, Can SIR be as popular as multiple linear
regression, Statist. Sinica 8 (1998), 289-316.
[6] H. Chen, Convergence rates for parametric components in a partly
linear model, Ann. Statist. 16 (1988), 136-141.
[7] X. Chen, C. Zou and R. D. Kook, Coordinate-independent sparse
sufficient dimension reduction and variable selection, Ann. Statist.
38 (2010), 3696-3723.
[8] R. D. Cook and F. Critchley, Identifying regression outliers and
mixtures graphically, J. Amer. Statist. Assoc. 95 (2000), 781-794.
[9] R. D. Cook and S. Weisberg, Discussion of ‘sliced inverse
regression for dimension reduction by K. C. Li, J. Amer. Statist.
Assoc. 86 (1991), 328-332.
[10] R. D. Cook and L. Ni, Sufficient dimension reduction via inverse
regression: A minimum discrepancy approach, J. Amer. Statist. Assoc.
100 (2005), 410-428.
[11] P. Diaconis and D. Freedman, Asymptotics of graphical projection
pursuit, Ann. Statist. 12 (1984), 793-815.
[12] K. Doksum and J. Y. Koo, On spline estimators and prediction
intervals in nonparametric regression, Comput. Statist. & Data Anal.
35 (2000), 67-82.
[13] J. Fan and R. Li, Variable selection via nonconcave penalized
likelihood and its oracle properties, J. Amer. Statist. Assoc. 96
(2001), 1348-1360.
[14] I. E. Frank and J. H. Friedman, A statistical view of some
chemometrics regression tools (with discussion), Technometrics 35
(1993), 109-148.
[15] W. Härdle, Hua Liang and J. Gao, Partially Linear Models,
Springer, New York, 2000.
[16] D. Harrison and D. Rubinfeld, Hedonic housing pries and the
demand for clean air, Journal of Environmental Economics and
Management 5 (1978), 81-102.
[17] X. He and B. Shi, Bivariate tensor-product B-splines in a
partially linear regression, J. Multivariate Anal. 58 (1996),
162-181.
[18] N. Heckman, Spline smoothing in a partly linear model, J. Roy.
Statist. Soc. Ser. A 48 (1986), 244-248.
[19] T. Hoshino, Quantile regression estimation of partially linear
additive models, Journal of Nonparametric Statistics 26 (2014),
509-536.
[20] W. Jiang, H. D. Bondell and H. J. Wang, Interquantile shrinkage
and variable selection in quantile regression, Comput. Statist. & Data
Anal. 69 (2014), 208-219.
[21] K. Knight, Limiting distributions for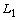 
regression estimators under general
conditions, Ann. Statist. 26 (1998), 755-770.
[22] R. Koenker and G. Bassett, Regression quantiles, Econometrica 46
(1978), 33-50.
[23] R. Koenker and N. S. Portnoy, Quantile smoothing splines,
Biometrika 81 (1994), 673-680.
[24] S. Lee, Efficient semiparametric estimation of a partially linear
quantile regression model, Econometric Theory 19 (2003), 1-31.
[25] K. C. Li, Sliced inverse regression for dimension reduction, J.
Amer. Statist. Assoc. 102 (1991), 997-1008.
[26] K. C. Li, On principal Hessian directions for data visualization
and dimension reduction: Another application of Stein’s lemma,
J. Amer. Statist. Assoc. 87 (1992), 1025-1039.
[27] L. Li, Sparse sufficient dimension reduction, Biometrika 94
(2007), 603-613.
[28] B. Li and S. Wang, On directional regression for dimension
reduction, J. Amer. Statist. Assoc. 33 (2007), 1580-1616.
[29] Y. Li and L. X. Zhu, Asymptotics for sliced average variance
estimation, Ann. Statist. 35 (2007), 41-69.
[30] Y. Li and L. J. Zhu,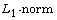 
quantile regression, J. Comput. Graph.
Statist. 17 (2008), 163-185.
[31] X. Liu, L. Wang and H. Liang, Estimation and variable selection
for semiparametric additive partial linear models, Stat. Sin. 21
(2011), 1225-1248.
[32] Y. Ma and L. Zhu, On estimation efficiency of the central mean
subspace, J. Roy. Statist. Soc. B 76 (2014), 885-901.
[33] D. Pollard, Asymptotics for least absolute deviation regression
estimators, Econometric Theory 7 (1991), 186-199.
[34] P. T. Reiss and L. Huang, Smoothness selection for penalized
quantile regression splines, The International Journal of
Biostatistics (2012), 8-1.
[35] D. Ruppert, M. P. Wand and R. J. Carroll, Semiparametric
Regression, Cambridge Univ. Press, New York, 2003.
[36] Y. Sun, Semiparametric efficient estimation of partially linear
quantile regression models, Annals of Economics and Finance 6 (2005),
105-127.
[37] R. Tibshirani, Regression shrinkage and selection via the lasso,
J. Roy. Statist. Soc. Ser. B 58 (1996), 267-288.
[38] D. Tyler, Asymptotic inference for eigenvectors, Ann. Stat. 9
(1981), 725-736.
[39] S. N. Wood, Thin plate regression splines, J. R. Statist. Soc. B
65 (2003), 95-114.
[40] Y. Wu and Y. Liu, Variable selection in quantile regression,
Statistica Sinica 19 (2009), 801-817.
[41] Y. Xia and W. Härdle, Semi-parametric estimation of partially
linear single-index models, J. Multivariate Anal. 97 (2006),
1162-1184.
[42] Y. Xia, H. Tong, W. K. Li and L. X. Zhu, An adaptive estimation
of dimension reduction space, J. Roy. Statist. Soc. Ser. B 64 (2002),
363-410.
[43] Luo Xiao, Y. Li and D. Ruppert, Fast bivariate P-splines:
The Sandwich smoother, J. Roy. Statist. Soc. B 75 (2013),
577-599.
[44] Z. Ye and R. E. Weiss, Using the bootstrap to select one of a new
class of dimension reduction methods, J. Amer. Statist. Assoc. 98
(2003), 968-979.
[45] P. Yoo and R. D. Cook, Optimal sufficient dimension reduction for
the conditional mean in multivariate regressions, Biometrika 94
(2007), 231-242.
[46] T. Yoshida, Partially linear estimation using sufficient
dimension reduction, Submitted (2015).
[47] L. X. Zhu and K. W. Ng, Asymptotics of sliced inverse regression,
Statist. Sinica 5 (1995), 727-736.
[48] L. X. Zhu, B. Q. Miao and H. Peng, Sliced inverse regression with
large-dimensional covariates, J. Amer. Statist. Assoc. 101 (2006),
630-643.
[49] L. P. Zhu, R. Li and H. Cui, Robust estimation for partially
linear models with large-dimensional covariates, Science China
Mathematics 56 (2013), 2069-2088.
[50] H. Zou, The adaptive lasso and its oracle properties, J. Amer.
Statist. Assoc. 101 (2006), 1418-1429.
